第 2 章 基本数据操作
在金融数据分析中，任何策略的研发与验证都始于标准化的数据操作，这就如同建筑施工前必须夯实地基 ——quantmod 包通过系统化的函数分类，将数据处理逻辑拆解为可复用的功能模块。考虑到按字母顺序学习函数会割裂业务关联性，更科学的方式是按功能用途分组，其中逻辑判断类、数据提取类、时期转换类等模块构成了量化分析的基础工具链。
2.1 验证数据的函数
为何需要验证函数？这源于 quantmod 包对数据格式的严格要求 —— 其核心功能仅支持OHLC（开盘价 / 最高价 / 最低价 / 收盘价）、OHLCV（含成交量）、BBO（最优买卖报价）等特定格式，若输入数据不符合规范，后续计算将面临错误风险。因此，逻辑判断类函数承担着数据预处理的 “守门人” 角色，在执行任何分析前校验数据格式的合规性，避免因格式不匹配导致的全流程误差。
这类函数可细分为两大体系：is.* 类类型验证函数与 **has.类完整性验证函数*，二者协同完成数据质量把控。前者（如 is.OHLC、is.quantmod）用于判断数据是否属于特定格式类型，后者（如 has.OHLC、has.Vo）则检测数据中是否包含指定维度的指标列。例如： 当从不同数据源导入股票数据时，先通过 is.OHLCV 验证是否包含完整的开盘价 / 成交量等列； 若数据列名不规范（如小写的 “open” 而非 “Open”），需借助 has.Op 函数定位缺失列并通过 colnames 重命名。
is.* 与 has.* 函数的组合使用形成了数据校验的双重防线：前者从整体格式层面判断数据是否为 quantmod 兼容类型（如 xts 时间序列），后者则从细节维度检测具体指标的完整性（如是否存在调整后收盘价列）。以获取 AAPL 股票数据为例：
## [1] "AAPL"if (is.quantmod(AAPL) && has.OHLCV(AAPL)) {
# 执行后续分析（如收益率计算）
dailyRet <- dailyReturn(Cl(AAPL))
# 打印前五行数据
head(dailyRet)
} else {
# 触发数据清洗流程（如重命名列名或填充缺失值）
AAPL=as.quantmod.OHLC(AAPL)
print("已完成数据清洗")
}## [1] "已完成数据清洗"这种先校验后操作的流程，能将格式错误排查提前至预处理阶段，尤其在处理多源异构数据（如整合美股与加密货币数据）时，可通过逻辑判断函数快速识别格式差异，避免因数据结构混乱导致的策略误判。从本质上看，逻辑判断类函数不仅是技术工具，更是量化分析中 “数据质量优先” 原则的实现载体，确保后续的指标计算、策略回测建立在可靠的数据基础之上。
2.1.1 验证数据类型
在量化分析中，确保金融数据符合特定格式规范是避免计算错误的关键环节。quantmod 包提供的 is.* 类函数如同数据格式的 “守门人”，通过严格的类型校验机制，帮助分析师快速识别数据结构的合规性。这些函数以统一的命名规范实现对不同维度金融数据的类型验证，核心作用在于提前规避因数据格式不匹配导致的后续计算异常。
is.OHLC (x) 用于判断数据是否包含标准的开盘价、最高价、最低价、收盘价四列（列名需严格遵循 Open/High/Low/Close 的大写规范），而 is.OHLCV (x) 在此基础上增加对成交量列的校验。
对于仅需价格波动分析的场景，is.HLC (x) 可检测数据是否包含最高价、最低价、收盘价三列。在市场报价数据中，is.BBO (x) 和 is.TBBO (x) 用于验证是否包含最优买卖报价（Best Bid and Offer）及时间戳买卖报价数据，这类函数在高频交易或订单簿分析中尤为重要。
此外，is.quantmod (x) 用于判断数据是否为 quantmod 兼容的格式（如 xts 时间序列），而 is.quantmodResults (x) 则专门校验数据是否为 quantmod 内部函数的输出结果（如 getSymbols 返回的结构化列表）。
使用这些函数时需注意三大要点：列名规范性是首要前提，若数据列名不符合 Open/High 等大写规范（如写成 open/high），需通过 colnames () 提前重命名，否则会导致校验失败；xts 格式依赖性决定了非 xts 格式的数据（如普通 data.frame）可能触发错误，建议在数据导入时统一转换为 xts 格式；is.quantmodResults 的特殊性体现在其对内部结构的严格要求 —— 该函数通常用于验证 getSymbols 等函数的输出（需包含 call、symbol 等元数据属性），自定义对象需满足特定字段规范才能通过校验。
以苹果公司股票数据为例，从 Yahoo Finance 获取的 AAPL 数据可通过以下方式校验：
## [1] "AAPL"## [1] TRUE# 检查对象是否符合OHLCV格式(Open, High, Low, Close, Volume)
# 返回TRUE表示数据包含完整的开盘价、最高价、最低价、收盘价和成交量
is.OHLCV(AAPL)## [1] TRUE## [1] TRUE##市场报价数据验证
# 检查对象是否符合BBO格式(Best Bid and Offer)
# 返回FALSE，因为BBO格式需要买卖报价数据，而getSymbols默认获取的是OHLCV数据
is.BBO(AAPL)## [1] FALSE# quantmod 包相关类型验证
# 检查对象是否为quantmod包支持的格式
# 返回TRUE，因为getSymbols生成的是quantmod兼容的xts时间序列对象
is.quantmod(AAPL)## [1] FALSE这类验证在实际应用中具有多重价值：当整合多源数据时，可通过 is.OHLCV 快速识别缺失维度（如某数据源无成交量列）；在策略回测前，使用 is.quantmodResults 校验数据结构，能避免因格式不兼容导致的模型运行错误；而对 BBO 数据的校验，则为高频交易策略的订单簿分析奠定了数据基础。通过系统化的类型验证，量化分析师可将数据格式错误排查提前至预处理阶段，有效提升策略研发的效率与可靠性。
2.1.2 验证数据完整性
在量化分析中，确保金融数据的完整性是策略研发的前提，quantmod 包提供的验证函数可精准检测数据中各维度指标的存在性，避免因数据缺失导致分析偏差。这些函数以has.为前缀，通过统一的参数设计实现对 OHLCV、价格、成交量等不同维度的校验。
验证函数的基本语法为：
has.*(x, which = FALSE) 其中, x 为待检查的 xts 或 data.frame 格式数据；which 参数控制返回形式：当 which = FALSE（默认）时，返回 TRUE/FALSE 判断指定列是否存在；当which = TRUE时，返回实际存在的列名（如 has.OHLC(AAPL, which = TRUE 会列出 AAPL 数据中包含的 OHLC 列）。
对于单列数据的精细化校验，has.Op(x)、has.Hi(x)、has.Lo(x)、has.Cl(x)、has.Vo(x)、has.Ad(x)分别用于检测开盘价、最高价、最低价、收盘价、成交量和调整后收盘价的存在性。
在交易数据场景中，has.Ask(x) 和has.Bid(x)可验证买卖报价列是否存在，has.Price(x) 适用于单一价格数据的校验，而has.Qty(x) 和has.Trade(x) 则用于检查交易数量和完整交易记录列（如成交时间、价格、数量）的完整性。
典型应用如：
## [1] TRUE## [1] TRUE## [1] TRUE## [1] TRUE## [1] TRUE## [1] TRUE## [1] FALSE## [1] FALSE## [1] FALSE## [1] FALSE## [1] FALSE在价格数据校验中，has.OHLC(x)用于验证数据是否包含完整的开盘价、最高价、最低价、收盘价四列，has.HLC(x)则聚焦于最高价、最低价、收盘价三列的存在性，而has.OHLCV(x)可同时检查 OHLC 五维数据（含成交量）的完整性。例如：
## [1] TRUE TRUE TRUE TRUE## [1] TRUE TRUE TRUE## [1] TRUE TRUE TRUE TRUE TRUE这些验证函数在数据预处理阶段至关重要：当从不同数据源导入数据时，可通过 has.* 函数快速识别缺失维度（如某数据源未提供成交量数据），避免因列名不一致或数据缺失导致的计算错误；在策略回测前，使用 which=TRUE 参数可精准定位缺失列，为数据清洗（如填充缺失值或丢弃无效数据）提供依据。通过系统化的数据完整性校验，量化分析师能确保后续的指标计算（如收益率、波动率）和策略回测建立在可靠的数据基础上，从源头规避因数据质量问题导致的策略误判。
2.2 提取数据
在量化分析中，高效提取金融数据的核心指标是策略研发的基础。quantmod 包提供了一套标准化的数据提取函数，可从 xts 格式的 OHLCV（开盘价、最高价、最低价、收盘价、成交量）数据中精准分离各类关键信息。
Op(x)、Hi(x)、Lo(x)、Cl(x)、Vo(x)和Ad(x)分别用于提取开盘价、最高价、最低价、收盘价、成交量和调整后收盘价。以苹果公司股票数据为例，Op(AAPL)可直接获取 AAPL 的开盘价序列，帮助分析开盘阶段的多空力量；Cl(AAPL)提取的收盘价是技术分析中最关键的指标，常用于计算收益率和构建趋势线；Ad(AAPL)则考虑了股息、拆股等因素，提供更真实的价格基准。这些函数通过简洁的语法实现了数据的精准分离，例如Vo(AAPL)能快速定位成交量变化，为量价关系分析提供支持。
## AAPL.Open
## 2007-01-03 3.082
## 2007-01-04 3.002
## 2007-01-05 3.063
## 2007-01-08 3.070
## 2007-01-09 3.088
## 2007-01-10 3.384
## 2007-01-11 3.426
## 2007-01-12 3.378
## 2007-01-16 3.417
## 2007-01-17 3.484
## ...
## 2025-06-25 201.450
## 2025-06-26 201.430
## 2025-06-27 201.890
## 2025-06-30 202.010
## 2025-07-01 206.670
## 2025-07-02 208.910
## 2025-07-03 212.150
## 2025-07-07 212.680
## 2025-07-08 210.100
## 2025-07-09 209.530## AAPL.High
## 2007-01-03 3.092
## 2007-01-04 3.070
## 2007-01-05 3.079
## 2007-01-08 3.090
## 2007-01-09 3.321
## 2007-01-10 3.493
## 2007-01-11 3.456
## 2007-01-12 3.395
## 2007-01-16 3.473
## 2007-01-17 3.486
## ...
## 2025-06-25 203.670
## 2025-06-26 202.640
## 2025-06-27 203.220
## 2025-06-30 207.390
## 2025-07-01 210.190
## 2025-07-02 213.340
## 2025-07-03 214.650
## 2025-07-07 216.230
## 2025-07-08 211.430
## 2025-07-09 211.330## AAPL.Low
## 2007-01-03 2.925
## 2007-01-04 2.994
## 2007-01-05 3.014
## 2007-01-08 3.046
## 2007-01-09 3.041
## 2007-01-10 3.338
## 2007-01-11 3.396
## 2007-01-12 3.330
## 2007-01-16 3.409
## 2007-01-17 3.386
## ...
## 2025-06-25 200.620
## 2025-06-26 199.460
## 2025-06-27 200.000
## 2025-06-30 199.260
## 2025-07-01 206.140
## 2025-07-02 208.140
## 2025-07-03 211.810
## 2025-07-07 208.800
## 2025-07-08 208.450
## 2025-07-09 207.220## AAPL.Close
## 2007-01-03 2.993
## 2007-01-04 3.059
## 2007-01-05 3.037
## 2007-01-08 3.053
## 2007-01-09 3.306
## 2007-01-10 3.464
## 2007-01-11 3.421
## 2007-01-12 3.379
## 2007-01-16 3.468
## 2007-01-17 3.391
## ...
## 2025-06-25 201.560
## 2025-06-26 201.000
## 2025-06-27 201.080
## 2025-06-30 205.170
## 2025-07-01 207.820
## 2025-07-02 212.440
## 2025-07-03 213.550
## 2025-07-07 209.950
## 2025-07-08 210.010
## 2025-07-09 211.140## AAPL.Volume
## 2007-01-03 1.238e+09
## 2007-01-04 8.473e+08
## 2007-01-05 8.347e+08
## 2007-01-08 7.971e+08
## 2007-01-09 3.349e+09
## 2007-01-10 2.953e+09
## 2007-01-11 1.440e+09
## 2007-01-12 1.313e+09
## 2007-01-16 1.244e+09
## 2007-01-17 1.646e+09
## ...
## 2025-06-25 3.953e+07
## 2025-06-26 5.080e+07
## 2025-06-27 7.319e+07
## 2025-06-30 9.191e+07
## 2025-07-01 7.879e+07
## 2025-07-02 6.794e+07
## 2025-07-03 3.496e+07
## 2025-07-07 5.023e+07
## 2025-07-08 4.285e+07
## 2025-07-09 4.868e+07## AAPL.Adjusted
## 2007-01-03 2.519
## 2007-01-04 2.574
## 2007-01-05 2.556
## 2007-01-08 2.569
## 2007-01-09 2.782
## 2007-01-10 2.915
## 2007-01-11 2.879
## 2007-01-12 2.844
## 2007-01-16 2.918
## 2007-01-17 2.854
## ...
## 2025-06-25 201.560
## 2025-06-26 201.000
## 2025-06-27 201.080
## 2025-06-30 205.170
## 2025-07-01 207.820
## 2025-07-02 212.440
## 2025-07-03 213.550
## 2025-07-07 209.950
## 2025-07-08 210.010
## 2025-07-09 211.140对于需要同时获取多个价格维度的场景，HLC(x)和OHLC(x)函数可大幅提升数据处理效率。HLC(AAPL)会返回包含最高价、最低价和收盘价三列的 xts 对象，适用于绘制蜡烛图或计算波动指标（如布林带）；OHLC(AAPL)则提取开盘价、最高价、最低价和收盘价四列数据，完整保留交易日的价格波动轨迹，是技术指标计算的基础输入（如 MACD、RSI 等指标均依赖 OHLC 数据）。这种组合提取方式避免了多次调用单指标函数的繁琐操作，尤其在处理大规模历史数据时，能显著优化计算性能。
## AAPL.High AAPL.Low AAPL.Close
## 2007-01-03 3.092 2.925 2.993
## 2007-01-04 3.070 2.994 3.059
## 2007-01-05 3.079 3.014 3.037
## 2007-01-08 3.090 3.046 3.053
## 2007-01-09 3.321 3.041 3.306
## 2007-01-10 3.493 3.338 3.464
## 2007-01-11 3.456 3.396 3.421
## 2007-01-12 3.395 3.330 3.379
## 2007-01-16 3.473 3.409 3.468
## 2007-01-17 3.486 3.386 3.391
## ...
## 2025-06-25 203.670 200.620 201.560
## 2025-06-26 202.640 199.460 201.000
## 2025-06-27 203.220 200.000 201.080
## 2025-06-30 207.390 199.260 205.170
## 2025-07-01 210.190 206.140 207.820
## 2025-07-02 213.340 208.140 212.440
## 2025-07-03 214.650 211.810 213.550
## 2025-07-07 216.230 208.800 209.950
## 2025-07-08 211.430 208.450 210.010
## 2025-07-09 211.330 207.220 211.140## AAPL.Open AAPL.High AAPL.Low
## 2007-01-03 3.082 3.092 2.925
## 2007-01-04 3.002 3.070 2.994
## 2007-01-05 3.063 3.079 3.014
## 2007-01-08 3.070 3.090 3.046
## 2007-01-09 3.088 3.321 3.041
## 2007-01-10 3.384 3.493 3.338
## 2007-01-11 3.426 3.456 3.396
## 2007-01-12 3.378 3.395 3.330
## 2007-01-16 3.417 3.473 3.409
## 2007-01-17 3.484 3.486 3.386
## ...
## 2025-06-25 201.450 203.670 200.620
## 2025-06-26 201.430 202.640 199.460
## 2025-06-27 201.890 203.220 200.000
## 2025-06-30 202.010 207.390 199.260
## 2025-07-01 206.670 210.190 206.140
## 2025-07-02 208.910 213.340 208.140
## 2025-07-03 212.150 214.650 211.810
## 2025-07-07 212.680 216.230 208.800
## 2025-07-08 210.100 211.430 208.450
## 2025-07-09 209.530 211.330 207.220
## AAPL.Close
## 2007-01-03 2.993
## 2007-01-04 3.059
## 2007-01-05 3.037
## 2007-01-08 3.053
## 2007-01-09 3.306
## 2007-01-10 3.464
## 2007-01-11 3.421
## 2007-01-12 3.379
## 2007-01-16 3.468
## 2007-01-17 3.391
## ...
## 2025-06-25 201.560
## 2025-06-26 201.000
## 2025-06-27 201.080
## 2025-06-30 205.170
## 2025-07-01 207.820
## 2025-07-02 212.440
## 2025-07-03 213.550
## 2025-07-07 209.950
## 2025-07-08 210.010
## 2025-07-09 211.140这些提取函数的核心价值在于构建标准化的数据接口：单指标函数可精准定位特定维度（如通过Lo(x)识别历史支撑位），而组合函数则为综合分析提供结构化数据。例如，在计算真实波幅（ATR）时，需同时使用Hi(x)、Lo(x)和Cl(x)，此时HLC(x)可一次性获取所需数据；在回测趋势策略时，OHLC(x)提取的价格序列能直接用于移动平均线计算。通过灵活搭配这些函数，量化分析师可从原始金融数据中快速剥离有效信息，为后续的策略开发、绩效评估和风险建模奠定数据基础。
2.3 数据的简单计算
在 quantmod 包中，Delt 函数是计算金融数据变化率的核心工具，支持多种收益率计算逻辑，其基本语法为：
Delt(x1, x2 = NULL, k = 0, type = c("arithmetic", "log"))。该函数通过灵活的参数设计，实现了基础时间序列与对比序列的动态计算，广泛应用于收益率分析、波动率建模和交易信号生成等场景。
函数的核心参数中，x1 作为基础时间序列（如股票收盘价、开盘价），构成计算的基准；x2 为可选的对比序列，若不指定则默认使用 x1 的滞后值（由k 控制滞后阶数）。例如，当 k=1 时，Delt(Cl(x)) 等价于计算当日收盘价与前一日收盘价的变化率。type 参数决定收益率类型：选择 “arithmetic” 时计算算术收益率（(x1 - x2)/x2），适用于短期收益分析；选择 “log” 时计算对数收益率（log (x1/x2)），具有可加性优势，更适合长期复利计算和风险模型构建。
实际应用中，Delt 函数的灵活性体现在多维度计算场景：计算日收益率时，Delt(Cl(AAPL))可直接得出算术收益率；若需计算对数收益率，只需设置type=“log”；而当需要比较开盘价与收盘价的日内差异时，Delt(Op(AAPL), Cl(AAPL))能快速得出开盘至收盘的价格变化率。此外，通过k参数设置滞后阶数（如k=5），可计算 5 日前至当前的累积收益率，为跨周期分析提供支持。
该函数的底层逻辑为量化策略提供了标准化的变化率计算接口，无论是构建技术指标（如 MACD 的差值计算）、评估策略绩效（如日收益率序列生成），还是进行风险分析（如波动率估算），Delt 函数都能通过参数调整满足不同场景需求，成为连接原始价格数据与量化分析的关键桥梁。
创建一个包含 7 天股票开盘价和收盘价的示例数据集如表 2.1 所示：
# 定义价格数据
Stock.Open <- c(102.25, 102.87, 102.25, 100.87, 103.44, 103.87, 103.00)
Stock.Close <- c(102.12, 102.62, 100.12, 103.00, 103.87, 103.12, 105.12)
# 创建数据框
price_data <- data.frame(
日期 = seq(from = as.Date("2023-01-01"), length.out = 7, by = "day"),
开盘价 = Stock.Open,
收盘价 = Stock.Close
)| 日期 | 开盘价 | 收盘价 |
|---|---|---|
| 2023-01-01 | 102.2 | 102.1 |
| 2023-01-02 | 102.9 | 102.6 |
| 2023-01-03 | 102.2 | 100.1 |
| 2023-01-04 | 100.9 | 103.0 |
| 2023-01-05 | 103.4 | 103.9 |
| 2023-01-06 | 103.9 | 103.1 |
| 2023-01-07 | 103.0 | 105.1 |
计算算术收益率，即每日开盘价相对于前一日的变化率：
## [1] "使用Delt函数计算的日收益率:"## Delt.1.arithmetic
## [1,] NA
## [2,] 0.006064
## [3,] -0.006027
## [4,] -0.013496
## [5,] 0.025478
## [6,] 0.004157
## [7,] -0.008376## [1] "使用基础R函数计算的日收益率:"## [1] 0.006064 -0.006027 -0.013496 0.025478
## [5] 0.004157 -0.008376## [1] "Lengths: 7, 6"
## [2] "Attributes: < Modes: list, NULL >"
## [3] "Attributes: < Lengths: 2, 0 >"
## [4] "Attributes: < names for target but not for current >"
## [5] "Attributes: < current is not list-like >"
## [6] "target is matrix, current is numeric"计算对数收益率：
## [1] "使用Delt函数计算的对数收益率:"## Delt.1.log
## [1,] NA
## [2,] 0.006045
## [3,] -0.006045
## [4,] -0.013588
## [5,] 0.025159
## [6,] 0.004148
## [7,] -0.008411## [1] "使用基础R函数计算的对数收益率:"## [1] 0.006045 -0.006045 -0.013588 0.025159
## [5] 0.004148 -0.008411## [1] "Lengths: 7, 6"
## [2] "Attributes: < Modes: list, NULL >"
## [3] "Attributes: < Lengths: 2, 0 >"
## [4] "Attributes: < names for target but not for current >"
## [5] "Attributes: < current is not list-like >"
## [6] "target is matrix, current is numeric"计算开盘价与收盘价的差异：
## [1] "当日开盘-收盘差异率:"## Delt.0.arithmetic
## [1,] -0.001271
## [2,] -0.002430
## [3,] -0.020831
## [4,] 0.021116
## [5,] 0.004157
## [6,] -0.007221
## [7,] 0.020583## [1] "手动计算的当日开盘-收盘差异率:"## [1] 0.001271 0.002430 0.020831 -0.021116
## [5] -0.004157 0.007221 -0.020583## [1] "Attributes: < Modes: list, NULL >"
## [2] "Attributes: < Lengths: 2, 0 >"
## [3] "Attributes: < names for target but not for current >"
## [4] "Attributes: < current is not list-like >"
## [5] "target is matrix, current is numeric"计算开盘价与下一日收盘价的差异：
# 使用Delt函数计算开盘价与下一日收盘价的差异
interday_diff <- Delt(Stock.Open, Stock.Close, k = 1)
print("开盘价与下一日收盘价的差异率:")## [1] "开盘价与下一日收盘价的差异率:"## Delt.1.arithmetic
## [1,] NA
## [2,] 0.003619
## [3,] -0.026733
## [4,] 0.007335
## [5,] 0.029741
## [6,] -0.003094
## [7,] 0.012034# 等价的基础R实现
manual_interday <- (Stock.Open[1:6] - Stock.Close[2:7]) / Stock.Open[1:6]
print("手动计算的开盘价与下一日收盘价的差异率:")## [1] "手动计算的开盘价与下一日收盘价的差异率:"## [1] -0.003619 0.026733 -0.007335 -0.029741
## [5] 0.003094 -0.012034## [1] "Lengths: 7, 6"
## [2] "Attributes: < Modes: list, NULL >"
## [3] "Attributes: < Lengths: 2, 0 >"
## [4] "Attributes: < names for target but not for current >"
## [5] "Attributes: < current is not list-like >"
## [6] "target is matrix, current is numeric"我们比较一下不同收益率的差异。首先，计算不同方式计算的收益率数据：
# 加载必要的包
library(quantmod)
library(ggplot2)
library(dplyr)
library(tidyr)
# 获取AAPL数据
getSymbols("AAPL", from = "2025-01-01", to = Sys.Date())## [1] "AAPL"## AAPL.Open AAPL.High AAPL.Low
## 2025-01-02 248.9 249.1 241.8
## 2025-01-03 243.4 244.2 241.9
## 2025-01-06 244.3 247.3 243.2
## 2025-01-07 243.0 245.6 241.4
## 2025-01-08 241.9 243.7 240.1
## 2025-01-10 240.0 240.2 233.0
## AAPL.Close AAPL.Volume
## 2025-01-02 243.9 55740700
## 2025-01-03 243.4 40244100
## 2025-01-06 245.0 45045600
## 2025-01-07 242.2 40856000
## 2025-01-08 242.7 37628900
## 2025-01-10 236.9 61710900
## AAPL.Adjusted
## 2025-01-02 243.3
## 2025-01-03 242.8
## 2025-01-06 244.4
## 2025-01-07 241.6
## 2025-01-08 242.1
## 2025-01-10 236.3## An xts object on 2025-01-02 / 2025-07-09 containing:
## Data: double [128, 6]
## Columns: AAPL.Open, AAPL.High, AAPL.Low, AAPL.Close, AAPL.Volume ... with 1 more column
## Index: Date [128] (TZ: "UTC")
## xts Attributes:
## $ src : chr "yahoo"
## $ updated: POSIXct[1:1], format: ...# 计算算术收益率（日涨跌幅）
daily_returns <- Delt(Cl(AAPL)) # 使用收盘价计算
# 计算对数收益率
log_returns <- Delt(Cl(AAPL), type = "log")
# 计算日内差异率（收盘价 vs 开盘价）
intraday_diff <- Delt(Op(AAPL), Cl(AAPL))
# 合并所有收益率数据
returns_merged <- merge(daily_returns, log_returns, intraday_diff)
colnames(returns_merged) <- c("算术收益率", "对数收益率", "日内差异率")
# 移除缺失值
returns_merged <- na.omit(returns_merged)
# 转换为数据框
returns_df <- data.frame(
日期 = index(returns_merged),
coredata(returns_merged)
)
# 转换为长格式便于绘图
returns_long <- pivot_longer(
returns_df,
cols = -日期,
names_to = "收益率类型",
values_to = "收益率"
)# 创建可视化图表
p <- ggplot(returns_long,
aes(x = 日期,
y = 收益率,
color = 收益率类型)
) +
geom_line(linewidth = 0.8) +
geom_point(alpha = 0.5, size = 1.5) +
geom_hline(yintercept = 0,
linetype = "dashed",
color = "gray50") +
facet_wrap(~ 收益率类型,
ncol = 1,
scales = "free_y") +
labs(
title = "苹果公司(AAPL)不同类型收益率对比分析",
x = "日期",
y = "收益率",
caption = "数据来源: Yahoo Finance"
) +
theme_minimal() +
theme(
legend.position = "bottom",
plot.title = element_text(hjust = 0.5,
face = "bold",
size = 14),
strip.text = element_text(face = "bold",
size = 12),
axis.text.x = element_text(angle = 45,
hjust = 1)
)
print(p)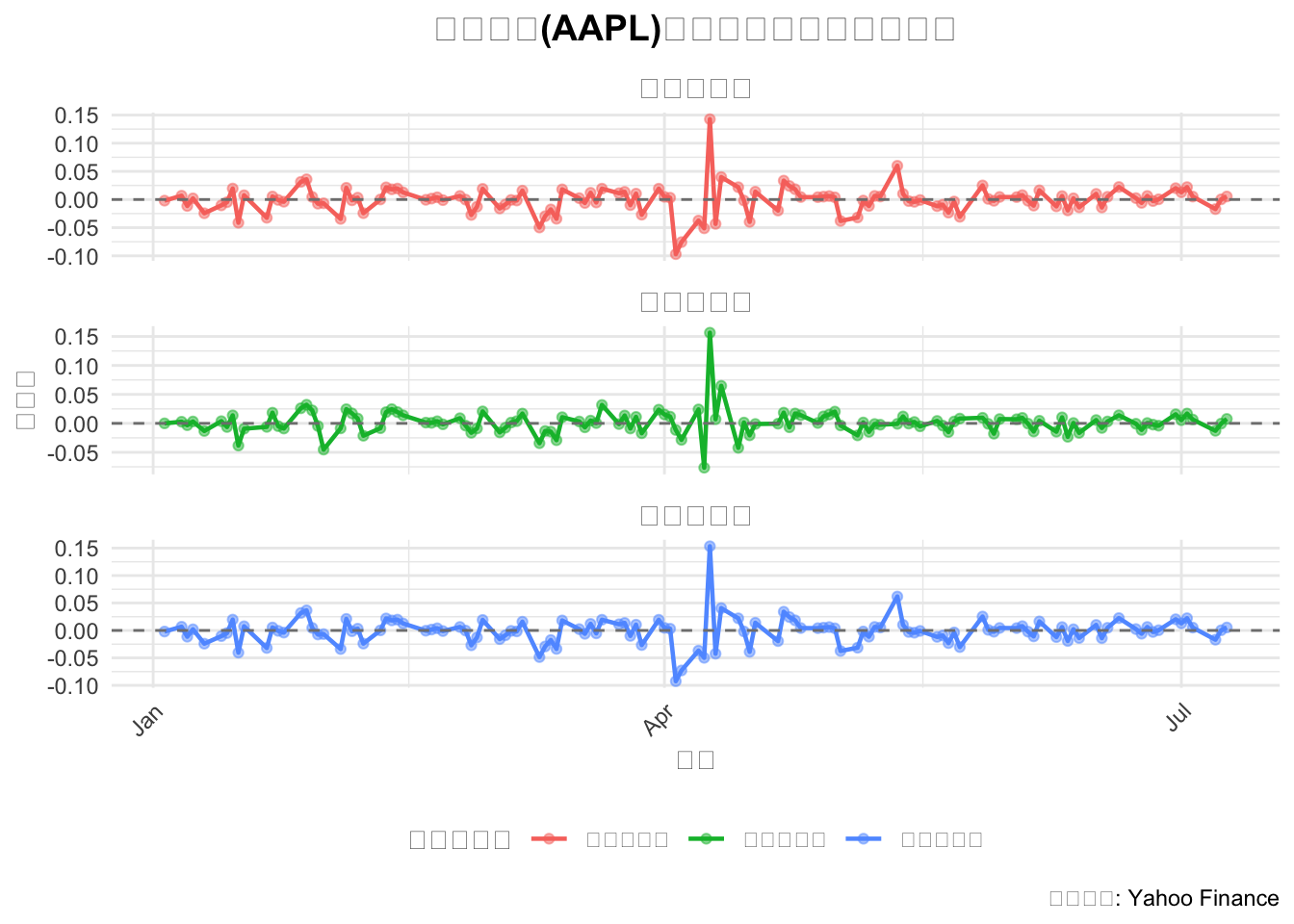
图 2.1: 苹果公司(AAPL)不同类型收益率对比分析
2.4 序列计算函数
在量化金融分析中，quantmod 包提供的序列计算函数通过挖掘价格序列的内在关系，为 K 线形态分析、波动率评估和趋势判断提供了底层工具。这些函数以价格差值或变化率为核心，将开盘价（Op）、收盘价（Cl）、最高价（Hi）、最低价（Lo）等基础数据转化为具有交易指导意义的指标。
OpCl(x) 函数通过计算开盘价与收盘价的差值（等价于 Delt (Op (x), Cl (x))），直接反映多空双方在一个交易周期内的力量对比：结果为正时，开盘价高于收盘价，对应 K 线形态中的阴线；结果为负时，收盘价高于开盘价，对应阳线。这一指标是 K 线形态识别的基础，能帮助分析师快速判断当日价格走势的强弱关系。
ClCl(x) 作为计算收盘价收益率的核心函数，等价于 Delt (Cl (x))，即相邻交易日收盘价的百分比变化（diff (Cl (x))/lag (Cl (x))）。该指标是量化策略中最基础的收益计算方式，常用于构建收益率序列、评估策略绩效或作为其他技术指标的输入参数，例如在计算波动率、夏普比率时，ClCl (x) 的输出是必不可少的基础数据。
HiCl(x) 和LoCl(x) 分别衡量最高价与收盘价、最低价与收盘价的偏离程度（等价于 Delt (Hi (x), Cl (x)) 和 Delt (Lo (x), Cl (x))）。前者反映价格上方的压力位强度， 当最高价远超收盘价时，说明上涨动能在收盘前被压制，可能形成上影线较长的 K 线；后者则评估下方支撑力度，最低价与收盘价的较大差值常对应下影线较长的 K 线，暗示价格在低位获得支撑。这两个指标结合 K 线形态，能辅助判断市场情绪转折的关键位置。
LoHi(x) 通过计算最低价与最高价的差值（Delt (Lo (x), Hi (x))），直接衡量价格波动范围。由于最低价通常小于最高价，该指标结果多为负值，但其绝对值越大，表明当日价格波动越剧烈，常用于波动率指标的构建（如真实波幅 ATR 的计算）或市场活跃度判断，帮助交易者调整仓位大小或止损范围。
OpHi(x) 和OpLo(x) 则聚焦于开盘后的价格走势：前者计算开盘价与最高价的差值（Delt (Op (x), Hi (x))），反映开盘后价格上涨的幅度，若结果为正且数值较大，说明开盘后多头迅速推高价格；后者计算开盘价与最低价的差值（Delt (Op (x), Lo (x))），体现开盘后价格下跌的幅度，负值越大表明开盘后空头力量占优。这两个指标对日内交易策略尤为重要，能帮助捕捉开盘后的短期趋势信号。
OpOp(x) 作为分析开盘价连续性的工具，等价于 Delt (Op (x))，通过计算相邻交易日开盘价的变化率，识别开盘价的趋势性特征。当连续多个交易日的 OpOp (x) 为正且数值稳定时，常预示开盘价存在持续上升趋势，反之则可能形成下降趋势，这对跳空高开或低开的行情分析具有重要参考价值。
这些序列计算函数通过解构价格序列的不同维度关系，将原始交易数据转化为具有逻辑关联的分析指标，不仅是技术指标构建的基础（如 MACD、RSI 等指标的底层计算常依赖此类函数），也为量化策略提供了从价格现象到交易信号的转化桥梁。在实际应用中，结合多个指标的协同分析（如 OpCl (x) 判断 K 线阴阳、LoHi (x) 评估波动幅度、ClCl (x) 计算收益趋势），能更全面地把握市场动态，提升策略信号的可靠性。
## OpCl.AAPL
## 2025-01-02 -0.0204073
## 2025-01-03 0.0000000
## 2025-01-06 0.0028243
## 2025-01-07 -0.0031689
## 2025-01-08 0.0032242
## 2025-01-10 -0.0131661
## 2025-01-13 0.0037254
## 2025-01-14 -0.0062620
## 2025-01-15 0.0137658
## 2025-01-16 -0.0382979
## ...
## 2025-06-25 0.0005460
## 2025-06-26 -0.0021347
## 2025-06-27 -0.0040121
## 2025-06-30 0.0156428
## 2025-07-01 0.0055645
## 2025-07-02 0.0168972
## 2025-07-03 0.0065991
## 2025-07-07 -0.0128362
## 2025-07-08 -0.0004284
## 2025-07-09 0.0076839## ClCl.AAPL
## 2025-01-02 NA
## 2025-01-03 -0.0020095
## 2025-01-06 0.0067390
## 2025-01-07 -0.0113877
## 2025-01-08 0.0020230
## 2025-01-10 -0.0241038
## 2025-01-13 -0.0103442
## 2025-01-14 -0.0047781
## 2025-01-15 0.0196759
## 2025-01-16 -0.0404002
## ...
## 2025-06-25 0.0062905
## 2025-06-26 -0.0027783
## 2025-06-27 0.0003980
## 2025-06-30 0.0203401
## 2025-07-01 0.0129162
## 2025-07-02 0.0222308
## 2025-07-03 0.0052250
## 2025-07-07 -0.0168579
## 2025-07-08 0.0002858
## 2025-07-09 0.0053807## HiCl.AAPL
## 2025-01-02 -0.0210759
## 2025-01-03 -0.0033581
## 2025-01-06 -0.0094206
## 2025-01-07 -0.0136021
## 2025-01-08 -0.0041443
## 2025-01-10 -0.0137825
## 2025-01-13 -0.0011506
## 2025-01-14 -0.0120278
## 2025-01-15 -0.0045615
## 2025-01-16 -0.0409647
## ...
## 2025-06-25 -0.0103599
## 2025-06-26 -0.0080932
## 2025-06-27 -0.0105305
## 2025-06-30 -0.0107045
## 2025-07-01 -0.0112755
## 2025-07-02 -0.0042186
## 2025-07-03 -0.0051246
## 2025-07-07 -0.0290431
## 2025-07-08 -0.0067162
## 2025-07-09 -0.0008991## LoCl.AAPL
## 2025-01-02 0.008395
## 2025-01-03 0.006077
## 2025-01-06 0.007401
## 2025-01-07 0.003563
## 2025-01-08 0.011039
## 2025-01-10 0.016524
## 2025-01-13 0.020373
## 2025-01-14 0.003484
## 2025-01-15 0.014674
## 2025-01-16 0.001009
## ...
## 2025-06-25 0.004685
## 2025-06-26 0.007721
## 2025-06-27 0.005400
## 2025-06-30 0.029660
## 2025-07-01 0.008150
## 2025-07-02 0.020659
## 2025-07-03 0.008215
## 2025-07-07 0.005508
## 2025-07-08 0.007484
## 2025-07-09 0.018917## LoHi.AAPL
## 2025-01-02 0.030105
## 2025-01-03 0.009467
## 2025-01-06 0.016982
## 2025-01-07 0.017402
## 2025-01-08 0.015247
## 2025-01-10 0.030730
## 2025-01-13 0.021548
## 2025-01-14 0.015701
## 2025-01-15 0.019324
## 2025-01-16 0.043766
## ...
## 2025-06-25 0.015203
## 2025-06-26 0.015943
## 2025-06-27 0.016100
## 2025-06-30 0.040801
## 2025-07-01 0.019647
## 2025-07-02 0.024983
## 2025-07-03 0.013408
## 2025-07-07 0.035584
## 2025-07-08 0.014296
## 2025-07-09 0.019834## OpHi.AAPL
## 2025-01-02 0.000683
## 2025-01-03 0.003369
## 2025-01-06 0.012361
## 2025-01-07 0.010577
## 2025-01-08 0.007399
## 2025-01-10 0.000625
## 2025-01-13 0.004882
## 2025-01-14 0.005836
## 2025-01-15 0.018411
## 2025-01-16 0.002781
## ...
## 2025-06-25 0.011020
## 2025-06-26 0.006007
## 2025-06-27 0.006588
## 2025-06-30 0.026632
## 2025-07-01 0.017032
## 2025-07-02 0.021205
## 2025-07-03 0.011784
## 2025-07-07 0.016692
## 2025-07-08 0.006330
## 2025-07-09 0.008591## OpLo.AAPL
## 2025-01-02 -0.028562
## 2025-01-03 -0.006040
## 2025-01-06 -0.004543
## 2025-01-07 -0.006708
## 2025-01-08 -0.007730
## 2025-01-10 -0.029207
## 2025-01-13 -0.016315
## 2025-01-14 -0.009712
## 2025-01-15 -0.000895
## 2025-01-16 -0.039267
## ...
## 2025-06-25 -0.004120
## 2025-06-26 -0.009780
## 2025-06-27 -0.009362
## 2025-06-30 -0.013613
## 2025-07-01 -0.002564
## 2025-07-02 -0.003686
## 2025-07-03 -0.001603
## 2025-07-07 -0.018243
## 2025-07-08 -0.007853
## 2025-07-09 -0.011025## OpOp.AAPL
## 2025-01-02 NA
## 2025-01-03 -0.0223757
## 2025-01-06 0.0039037
## 2025-01-07 -0.0054439
## 2025-01-08 -0.0043625
## 2025-01-10 -0.0078952
## 2025-01-13 -0.0269989
## 2025-01-14 0.0052242
## 2025-01-15 -0.0004686
## 2025-01-16 0.0115496
## ...
## 2025-06-25 -0.0056271
## 2025-06-26 -0.0000993
## 2025-06-27 0.0022837
## 2025-06-30 0.0005944
## 2025-07-01 0.0230682
## 2025-07-02 0.0108386
## 2025-07-03 0.0155090
## 2025-07-07 0.0024982
## 2025-07-08 -0.0121308
## 2025-07-09 -0.0027130## AAPL.Open Delt.1.arithmetic
## 2025-01-02 5.08 NA
## 2025-01-03 0.00 -8.241e-06
## 2025-01-06 -0.69 2.769e-05
## 2025-01-07 0.77 -4.648e-05
## 2025-01-08 -0.78 8.352e-06
## 2025-01-10 3.16 -9.932e-05
## AAPL.High
## 2025-01-02 5.25
## 2025-01-03 0.82
## 2025-01-06 2.33
## 2025-01-07 3.34
## 2025-01-08 1.01
## 2025-01-10 3.312.5 计算收益率
在量化投资领域，计算收益率是评估策略有效性、衡量资产回报以及构建风险模型的核心环节。收益率不仅是衡量投资绩效的基础指标，更是风险收益比计算、资产配置优化和策略回测的核心输入。它能帮助投资者识别市场趋势、比较不同资产的获利能力，以及通过波动率分析控制持仓风险。
quantmod 包提供了一套完整的收益率计算函数，覆盖从日度到年度的多周期需求，为量化分析提供了标准化的工具支持。其中，periodReturn () 作为通用周期收益率函数，可根据指定周期（如 “daily” 日度、“weekly” 周度）计算算术或对数收益率，通过 compound 参数控制复利计算逻辑，既能处理已有的收益率序列，也能直接将价格序列转换为收益率。与之对应的 dailyReturn () 函数则专门用于日收益率计算，采用对数收益率公式（log (今日收盘价 / 昨日收盘价)），并自动处理交易日间隔，等价于 periodReturn (period=“daily”) 的快捷调用。针对周度和月度等低频周期，weeklyReturn () 默认以周五收盘价计算周收益率，可通过 indexAt 参数调整为周内其他时点；monthlyReturn () 则基于月末收盘价计算月收益率，支持 indexAt=“lastof” 等参数指定具体月末时点。quarterlyReturn () 和 annualReturn ()（与 yearlyReturn () 功能一致）分别按自然季度和自然年划分周期，前者以 3 个月为单位，后者以年为单位，均支持复利计算参数。
此外，allReturns () 作为非标准内置函数（常为自定义或扩展函数），主要用于一次性整合多周期收益率结果，方便投资者从不同时间维度分析回报特征，例如同时获取日、周、年收益率以评估策略的短期波动性和长期趋势稳定性。这些函数通过标准化的参数设计和多周期覆盖，使量化投资者能够高效计算各类收益率指标，为策略研发、绩效评估和风险控制提供数据支撑。
以下代码以苹果公司（AAPL）2020-2023 年股价数据为例，演示各函数的具体应用：
# 加载所需包(如未加载)
library(quantmod) # 获取股价数据
library(PerformanceAnalytics) # 收益率计算
library(xts) # 时间序列处理
# 获取AAPL股价数据（2020-2023年）
getSymbols("AAPL", from = "2020-01-01", to = "2023-12-31")## [1] "AAPL"# 提取收盘价并转换为xts格式
aapl_cl <- Cl(AAPL)
# 日收益率计算（两种方式等价）
aapl_daily_return1 <- dailyReturn(aapl_cl)
aapl_daily_return2 <- periodReturn(aapl_cl, period = "daily")
# 周收益率计算（默认周五收盘）
aapl_weekly_return <- weeklyReturn(aapl_cl)
# 月收益率计算
aapl_monthly_return <- monthlyReturn(aapl_cl)
# 季度收益率计算
aapl_quarterly_return <- quarterlyReturn(aapl_cl)
# 年收益率计算（两种函数等价）
aapl_annual_return1 <- annualReturn(aapl_cl)
aapl_annual_return2 <- yearlyReturn(aapl_cl)
# 自定义allReturns函数（示例整合多周期结果）
allReturns <- function(price_data) {
daily <- dailyReturn(price_data)
weekly <- weeklyReturn(price_data)
monthly <- monthlyReturn(price_data)
annual <- annualReturn(price_data)
# 合并结果（仅展示部分周期为例）
list(
daily_returns = daily,
weekly_returns = weekly,
annual_returns = annual
)
}
# 调用自定义函数
aapl_all_returns <- allReturns(aapl_cl)
# 展示部分结果（以年收益率为例）
print("AAPL年收益率（2020-2023）：")## [1] "AAPL年收益率（2020-2023）："## yearly.returns
## 2020-12-31 0.7671
## 2021-12-31 0.3382
## 2022-12-30 -0.2683
## 2023-12-29 0.48182.6 序列的滞后/前移与选取
在量化金融分析中，quantmod 包提供的序列滞后与选取函数是处理时间序列数据的核心工具，这些函数深度依赖 xts 包对时间标签的处理能力，广泛应用于收益率计算、特征工程和滚动分析等场景。其中，Lag (x, k) 函数用于将时间序列 x 向后移动 k 期，通过获取历史值来计算收益率或构建滞后特征，k 为正数时表示向后移动（如 Lag (x,1) 取前一日数据），负数则表示向前移动。Next (x, k=1) 函数则是将时间序列 x 向前移动 k 期以获取未来值，在回测中常用于模拟预测场景，但需严格避免未来数据泄露影响策略有效性。 first (x, k) 函数能够按时间顺序提取 x 的前 k 个数据点，既可以通过 k 指定具体数量，也能借助 timeFrame 参数按时间范围提取（如 “first 3 months”），常用于子集分析或模型初始化数据加载。last (x, k) 函数则用于提取时间序列 x 的后 k 个最新数据点，同样支持 k 值或 timeFrame 参数（如 “last 1 year”），在获取近期数据进行滚动窗口分析或实时指标计算时尤为实用。这些函数通过对时间序列的灵活移位和子集选取，为金融时间序列的动态分析和建模提供了基础支撑，使得分析师能够高效处理历史数据、构建滞后特征并实现滚动策略回测。
以下代码以苹果公司（AAPL）2023 年股价数据为例，展示各函数的具体应用：
# 加载所需包
library(quantmod) # 获取股价数据
library(xts) # 时间序列处理
# 获取AAPL 2023年股价数据
getSymbols("AAPL", from = "2023-01-01", to = "2023-12-31")## [1] "AAPL"# 提取收盘价并转换为xts格式
aapl_cl <- Cl(AAPL)
# 1. Lag(x, k)：滞后计算（以滞后1日和5日为例）
aapl_lag1 <- Lag(aapl_cl, k=1) # 滞后1日（昨日收盘价）
aapl_lag5 <- Lag(aapl_cl, k=5) # 滞后5日（5日前收盘价）
# 计算日收益率（等价于dailyReturn）
aapl_return <- (aapl_cl-aapl_lag1)/aapl_lag1
# 2. Next(x, k)：前移计算（以预测1日后价格为例）
aapl_next1 <- Next(aapl_cl, k=1) # 1日后收盘价（未来值）
# 注意：实际回测中使用Next可能导致数据泄露，仅用于演示
# 示例：计算"未来1日收益率"（现实中无法提前获取）
aapl_future_return <- (aapl_next1 - aapl_cl) / aapl_cl## Warning: Incompatible methods ("Ops.zoo",
## "Ops.xts") for "-"## Warning: Incompatible methods ("Ops.zoo",
## "Ops.xts") for "/"# 3. first(x, k)：取前k个观测值（以取前20个交易日为例）
aapl_first20 <- aapl_cl[1:20] # 正确提取前20个交易日数据
# 或按时间范围提取（如前3个月）
aapl_first3m <- window(aapl_cl, start = start(aapl_cl), end = "2023-03-31")
# 4. last(x, k)：取后k个观测值（取最后10个交易日）
aapl_last10 <- tail(aapl_cl, 10) # 使用tail函数提取最后10个交易日数据
# 取最近6个月数据
aapl_last6m <- window(aapl_cl, start = "2023-07-01", end = end(aapl_cl))
# 整合结果展示（修复后的代码）
# 创建一个与aapl_cl相同长度的向量，前20个值为aapl_first20，其余为NA
first20_extended <- rep(NA, length(aapl_cl))
first20_extended[1:20] <- coredata(aapl_first20)
first20_extended <- xts(first20_extended, index(aapl_cl))
# 整合结果展示
combined_data <- cbind(aapl_cl, aapl_lag1, aapl_lag5, first20_extended)
colnames(combined_data) <- c("当日收盘价", "昨日收盘价", "5日前收盘价", "前20日收盘价")
# 显示前10行数据
head(combined_data, 10)## 当日收盘价 昨日收盘价 5日前收盘价
## 2023-01-03 125.1 NA NA
## 2023-01-04 126.4 125.1 NA
## 2023-01-05 125.0 126.4 NA
## 2023-01-06 129.6 125.0 NA
## 2023-01-09 130.1 129.6 NA
## 2023-01-10 130.7 130.1 125.1
## 2023-01-11 133.5 130.7 126.4
## 2023-01-12 133.4 133.5 125.0
## 2023-01-13 134.8 133.4 129.6
## 2023-01-17 135.9 134.8 130.1
## 前20日收盘价
## 2023-01-03 125.1
## 2023-01-04 126.4
## 2023-01-05 125.0
## 2023-01-06 129.6
## 2023-01-09 130.1
## 2023-01-10 130.7
## 2023-01-11 133.5
## 2023-01-12 133.4
## 2023-01-13 134.8
## 2023-01-17 135.9## [1] "AAPL"## AAPL.Open AAPL.High AAPL.Low
## 2023-01-03 130.3 130.9 124.2
## 2023-01-04 126.9 128.7 125.1
## 2023-01-05 127.1 127.8 124.8
## 2023-01-06 126.0 130.3 124.9
## 2023-01-09 130.5 133.4 129.9
## 2023-01-10 130.3 131.3 128.1
## 2023-01-11 131.2 133.5 130.5
## 2023-01-12 133.9 134.3 131.4
## 2023-01-13 132.0 134.9 131.7
## 2023-01-17 134.8 137.3 134.1
## ...
## 2023-12-15 197.5 198.4 197.0
## 2023-12-18 196.1 196.6 194.4
## 2023-12-19 196.2 196.9 195.9
## 2023-12-20 196.9 197.7 194.8
## 2023-12-21 196.1 197.1 193.5
## 2023-12-22 195.2 195.4 193.0
## 2023-12-26 193.6 193.9 192.8
## 2023-12-27 192.5 193.5 191.1
## 2023-12-28 194.1 194.7 193.2
## 2023-12-29 193.9 194.4 191.7
## AAPL.Close AAPL.Volume
## 2023-01-03 125.1 112117500
## 2023-01-04 126.4 89113600
## 2023-01-05 125.0 80962700
## 2023-01-06 129.6 87754700
## 2023-01-09 130.1 70790800
## 2023-01-10 130.7 63896200
## 2023-01-11 133.5 69458900
## 2023-01-12 133.4 71379600
## 2023-01-13 134.8 57809700
## 2023-01-17 135.9 63646600
## ...
## 2023-12-15 197.6 128256700
## 2023-12-18 195.9 55751900
## 2023-12-19 196.9 40714100
## 2023-12-20 194.8 52242800
## 2023-12-21 194.7 46482500
## 2023-12-22 193.6 37122800
## 2023-12-26 193.1 28919300
## 2023-12-27 193.1 48087700
## 2023-12-28 193.6 34049900
## 2023-12-29 192.5 42628800
## AAPL.Adjusted
## 2023-01-03 123.5
## 2023-01-04 124.7
## 2023-01-05 123.4
## 2023-01-06 128.0
## 2023-01-09 128.5
## 2023-01-10 129.1
## 2023-01-11 131.8
## 2023-01-12 131.7
## 2023-01-13 133.0
## 2023-01-17 134.2
## ...
## 2023-12-15 196.1
## 2023-12-18 194.5
## 2023-12-19 195.5
## 2023-12-20 193.4
## 2023-12-21 193.3
## 2023-12-22 192.2
## 2023-12-26 191.6
## 2023-12-27 191.7
## 2023-12-28 192.2
## 2023-12-29 191.1## AAPL.Open AAPL.High AAPL.Low
## 2024-01-02 187.1 188.4 183.9
## 2024-01-03 184.2 185.9 183.4
## 2024-01-04 182.1 183.1 180.9
## 2024-01-05 182.0 182.8 180.2
## 2024-01-08 182.1 185.6 181.5
## 2024-01-09 183.9 185.1 182.7
## 2024-01-10 184.4 186.4 183.9
## 2024-01-11 186.5 187.1 183.6
## 2024-01-12 186.1 186.7 185.2
## 2024-01-16 182.2 184.3 180.9
## ...
## 2024-12-17 250.1 253.8 249.8
## 2024-12-18 252.2 254.3 247.7
## 2024-12-19 247.5 252.0 247.1
## 2024-12-20 248.0 255.0 245.7
## 2024-12-23 254.8 255.6 253.4
## 2024-12-24 255.5 258.2 255.3
## 2024-12-26 258.2 260.1 257.6
## 2024-12-27 257.8 258.7 253.1
## 2024-12-30 252.2 253.5 250.8
## 2024-12-31 252.4 253.3 249.4
## AAPL.Close AAPL.Volume
## 2024-01-02 185.6 82488700
## 2024-01-03 184.2 58414500
## 2024-01-04 181.9 71983600
## 2024-01-05 181.2 62303300
## 2024-01-08 185.6 59144500
## 2024-01-09 185.1 42841800
## 2024-01-10 186.2 46792900
## 2024-01-11 185.6 49128400
## 2024-01-12 185.9 40444700
## 2024-01-16 183.6 65603000
## ...
## 2024-12-17 253.5 51356400
## 2024-12-18 248.1 56774100
## 2024-12-19 249.8 60882300
## 2024-12-20 254.5 147495300
## 2024-12-23 255.3 40858800
## 2024-12-24 258.2 23234700
## 2024-12-26 259.0 27237100
## 2024-12-27 255.6 42355300
## 2024-12-30 252.2 35557500
## 2024-12-31 250.4 39480700
## AAPL.Adjusted
## 2024-01-02 184.3
## 2024-01-03 182.9
## 2024-01-04 180.6
## 2024-01-05 179.9
## 2024-01-08 184.2
## 2024-01-09 183.8
## 2024-01-10 184.8
## 2024-01-11 184.2
## 2024-01-12 184.6
## 2024-01-16 182.3
## ...
## 2024-12-17 252.9
## 2024-12-18 247.5
## 2024-12-19 249.2
## 2024-12-20 253.9
## 2024-12-23 254.7
## 2024-12-24 257.6
## 2024-12-26 258.4
## 2024-12-27 255.0
## 2024-12-30 251.6
## 2024-12-31 249.8## AAPL.Open AAPL.High AAPL.Low
## 2024-01-02 187.1 188.4 183.9
## 2024-01-03 184.2 185.9 183.4
## 2024-01-04 182.1 183.1 180.9
## 2024-01-05 182.0 182.8 180.2
## 2024-01-08 182.1 185.6 181.5
## 2024-01-09 183.9 185.1 182.7
## 2024-01-10 184.4 186.4 183.9
## 2024-01-11 186.5 187.1 183.6
## 2024-01-12 186.1 186.7 185.2
## 2024-01-16 182.2 184.3 180.9
## 2024-01-17 181.3 182.9 180.3
## 2024-01-18 186.1 189.1 185.8
## 2024-01-19 189.3 191.9 188.8
## 2024-01-22 192.3 195.3 192.3
## 2024-01-23 195.0 195.8 193.8
## 2024-01-24 195.4 196.4 194.3
## 2024-01-25 195.2 196.3 193.1
## 2024-01-26 194.3 194.8 191.9
## 2024-01-29 192.0 192.2 189.6
## 2024-01-30 190.9 191.8 187.5
## 2024-01-31 187.0 187.1 184.4
## AAPL.Close AAPL.Volume
## 2024-01-02 185.6 82488700
## 2024-01-03 184.2 58414500
## 2024-01-04 181.9 71983600
## 2024-01-05 181.2 62303300
## 2024-01-08 185.6 59144500
## 2024-01-09 185.1 42841800
## 2024-01-10 186.2 46792900
## 2024-01-11 185.6 49128400
## 2024-01-12 185.9 40444700
## 2024-01-16 183.6 65603000
## 2024-01-17 182.7 47317400
## 2024-01-18 188.6 78005800
## 2024-01-19 191.6 68741000
## 2024-01-22 193.9 60133900
## 2024-01-23 195.2 42355600
## 2024-01-24 194.5 53631300
## 2024-01-25 194.2 54822100
## 2024-01-26 192.4 44594000
## 2024-01-29 191.7 47145600
## 2024-01-30 188.0 55859400
## 2024-01-31 184.4 55467800
## AAPL.Adjusted
## 2024-01-02 184.3
## 2024-01-03 182.9
## 2024-01-04 180.6
## 2024-01-05 179.9
## 2024-01-08 184.2
## 2024-01-09 183.8
## 2024-01-10 184.8
## 2024-01-11 184.2
## 2024-01-12 184.6
## 2024-01-16 182.3
## 2024-01-17 181.4
## 2024-01-18 187.3
## 2024-01-19 190.2
## 2024-01-22 192.5
## 2024-01-23 193.8
## 2024-01-24 193.1
## 2024-01-25 192.8
## 2024-01-26 191.0
## 2024-01-29 190.3
## 2024-01-30 186.7
## 2024-01-31 183.1## AAPL.Open AAPL.High AAPL.Low
## 2024-01-02 187.1 188.4 183.9
## 2024-01-03 184.2 185.9 183.4
## 2024-01-04 182.1 183.1 180.9
## 2024-01-05 182.0 182.8 180.2
## 2024-01-08 182.1 185.6 181.5
## 2024-01-09 183.9 185.1 182.7
## 2024-01-10 184.4 186.4 183.9
## 2024-01-11 186.5 187.1 183.6
## 2024-01-12 186.1 186.7 185.2
## 2024-01-16 182.2 184.3 180.9
## ...
## 2024-08-19 225.7 226.0 223.0
## 2024-08-20 225.8 227.2 225.4
## 2024-08-21 226.5 228.0 225.1
## 2024-08-22 227.8 228.3 223.9
## 2024-08-23 225.7 228.2 224.3
## 2024-08-26 226.8 227.3 223.9
## 2024-08-27 226.0 228.9 224.9
## 2024-08-28 227.9 229.9 225.7
## 2024-08-29 230.1 232.9 228.9
## 2024-08-30 230.2 230.4 227.5
## AAPL.Close AAPL.Volume
## 2024-01-02 185.6 82488700
## 2024-01-03 184.2 58414500
## 2024-01-04 181.9 71983600
## 2024-01-05 181.2 62303300
## 2024-01-08 185.6 59144500
## 2024-01-09 185.1 42841800
## 2024-01-10 186.2 46792900
## 2024-01-11 185.6 49128400
## 2024-01-12 185.9 40444700
## 2024-01-16 183.6 65603000
## ...
## 2024-08-19 225.9 40687800
## 2024-08-20 226.5 30299000
## 2024-08-21 226.4 34765500
## 2024-08-22 224.5 43695300
## 2024-08-23 226.8 38677300
## 2024-08-26 227.2 30602200
## 2024-08-27 228.0 35934600
## 2024-08-28 226.5 38052200
## 2024-08-29 229.8 51906300
## 2024-08-30 229.0 52990800
## AAPL.Adjusted
## 2024-01-02 184.3
## 2024-01-03 182.9
## 2024-01-04 180.6
## 2024-01-05 179.9
## 2024-01-08 184.2
## 2024-01-09 183.8
## 2024-01-10 184.8
## 2024-01-11 184.2
## 2024-01-12 184.6
## 2024-01-16 182.3
## ...
## 2024-08-19 225.1
## 2024-08-20 225.7
## 2024-08-21 225.6
## 2024-08-22 223.7
## 2024-08-23 226.0
## 2024-08-26 226.4
## 2024-08-27 227.2
## 2024-08-28 225.7
## 2024-08-29 229.0
## 2024-08-30 228.2## AAPL.Open AAPL.High AAPL.Low
## 2024-01-02 187.1 188.4 183.9
## 2024-01-03 184.2 185.9 183.4
## 2024-01-04 182.1 183.1 180.9
## 2024-01-05 182.0 182.8 180.2
## 2024-01-08 182.1 185.6 181.5
## 2024-01-09 183.9 185.1 182.7
## 2024-01-10 184.4 186.4 183.9
## 2024-01-11 186.5 187.1 183.6
## 2024-01-12 186.1 186.7 185.2
## 2024-01-16 182.2 184.3 180.9
## ...
## 2025-06-25 201.4 203.7 200.6
## 2025-06-26 201.4 202.6 199.5
## 2025-06-27 201.9 203.2 200.0
## 2025-06-30 202.0 207.4 199.3
## 2025-07-01 206.7 210.2 206.1
## 2025-07-02 208.9 213.3 208.1
## 2025-07-03 212.1 214.6 211.8
## 2025-07-07 212.7 216.2 208.8
## 2025-07-08 210.1 211.4 208.4
## 2025-07-09 209.5 211.3 207.2
## AAPL.Close AAPL.Volume
## 2024-01-02 185.6 82488700
## 2024-01-03 184.2 58414500
## 2024-01-04 181.9 71983600
## 2024-01-05 181.2 62303300
## 2024-01-08 185.6 59144500
## 2024-01-09 185.1 42841800
## 2024-01-10 186.2 46792900
## 2024-01-11 185.6 49128400
## 2024-01-12 185.9 40444700
## 2024-01-16 183.6 65603000
## ...
## 2025-06-25 201.6 39525700
## 2025-06-26 201.0 50799100
## 2025-06-27 201.1 73188600
## 2025-06-30 205.2 91912800
## 2025-07-01 207.8 78788900
## 2025-07-02 212.4 67941800
## 2025-07-03 213.6 34955800
## 2025-07-07 209.9 50229000
## 2025-07-08 210.0 42848900
## 2025-07-09 211.1 48676300
## AAPL.Adjusted
## 2024-01-02 184.3
## 2024-01-03 182.9
## 2024-01-04 180.6
## 2024-01-05 179.9
## 2024-01-08 184.2
## 2024-01-09 183.8
## 2024-01-10 184.8
## 2024-01-11 184.2
## 2024-01-12 184.6
## 2024-01-16 182.3
## ...
## 2025-06-25 201.6
## 2025-06-26 201.0
## 2025-06-27 201.1
## 2025-06-30 205.2
## 2025-07-01 207.8
## 2025-07-02 212.4
## 2025-07-03 213.6
## 2025-07-07 209.9
## 2025-07-08 210.0
## 2025-07-09 211.1AAPL[1,]
# first(AAPL)
AAPL[1:5,]
# first(AAPL,5)
# 猜猜它们返回的结果
# first(AAPL, '3 weeks')
# last(AAPL, '-3 weeks')
# last(first(AAPL, '2 weeks'), '3 days')与其他函数结合：
结合merge函数合并滞后序列，构建多维度特征：
aapl_features <- merge(
收盘价 = aapl_cl,
滞后1日 = Lag(aapl_cl),
滞后5日 = Lag(aapl_cl, 5),
领先1日 = Next(aapl_cl)
)通过这些函数，可高效处理时间序列数据的历史滞后和未来预测需求，为金融分析、量化策略开发提供基础数据操作支持。
2.7 计算峰值/峰谷
在 quantmod 包中，findPeaks 和 findValleys 是用于检测时间序列数据中局部极值点的实用函数，在金融市场分析中常被用来识别价格转折点与趋势变化信号。其中，findPeaks 函数主要用于检测时间序列 x 中的局部极大值点（即峰值），其核心参数包括待检测的 xts 格式时间序列数据 x，以及用于筛选显著极值的阈值参数 thresh 。当 thresh 设为 0 时，函数会保留所有局部极大值点，而增大阈值（如 thresh=2）则仅会保留比相邻值大至少指定幅度的峰值，从而过滤掉小波动带来的噪音干扰。
与之对应的 findValleys 函数则用于检测时间序列 x 中的局部极小值点（即谷值），同样以 x 作为输入的时间序列数据，并通过 thresh 参数控制谷值的显著性，仅保留比相邻值小至少 thresh 的谷值点。这两个函数的核心价值在于帮助分析师从价格序列中定位具有市场意义的转折点，为技术分析中的支撑位、阻力位判断及交易信号生成提供数据支持，尤其在结合移动平均线、RSI 等其他技术指标时，能更精准地识别趋势变化与潜在的买卖时机。
以下代码以苹果公司（AAPL）2023 年股价数据为例（图：2.2），展示如何使用这两个函数识别价格转折点：
# 加载所需包
library(quantmod) # 获取股价数据和极值检测函数
library(ggplot2) # 高级绘图
library(PerformanceAnalytics) # 收益率计算
# 获取AAPL 2023年股价数据
getSymbols("AAPL", from = "2023-01-01", to = "2023-12-31")## [1] "AAPL"# 提取收盘价并转换为xts格式
aapl_cl <- Cl(AAPL)
# 1. 检测峰值（默认参数）
peaks_idx <- findPeaks(aapl_cl)
aapl_peaks <- aapl_cl[peaks_idx]
# 2. 检测谷值（默认参数）
valleys_idx <- findValleys(aapl_cl)
aapl_valleys <- aapl_cl[valleys_idx]
# 3. 带阈值的峰值检测（仅保留比相邻值高至少2美元的峰值）
peaks_high <- findPeaks(aapl_cl, thresh = 2)
aapl_peaks_high <- aapl_cl[peaks_high]
# 4. 带阈值的谷值检测（仅保留比相邻值低至少2美元的谷值）
valleys_low <- findValleys(aapl_cl, thresh = 2)
aapl_valleys_low <- aapl_cl[valleys_low]
# 5. 可视化峰值和谷值
plot(aapl_cl, main = "AAPL 2023年收盘价及极值点",
ylab = "价格(美元)", col = "gray", lwd = 1.5)
points(index(aapl_peaks), aapl_peaks, col = "red", pch = 16, cex = 0.8)
points(index(aapl_valleys), aapl_valleys, col = "blue", pch = 16, cex = 0.8)
legend("topleft", legend = c("收盘价", "峰值", "谷值"),
col = c("gray", "red", "blue"), pch = c(NA, 16, 16), lty = c(1, NA, NA))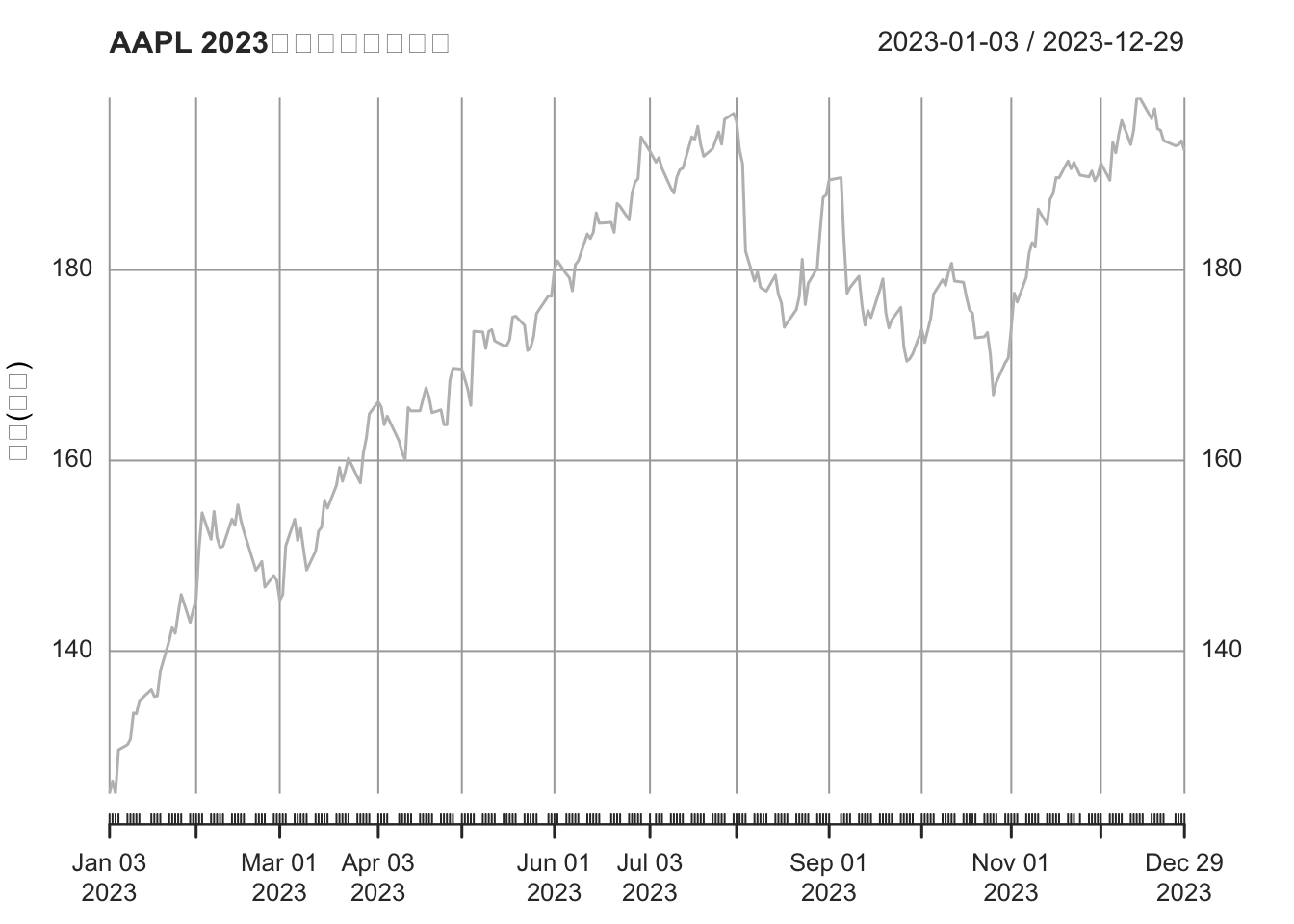
图 2.2: 苹果公司极值序列图
# 6. 计算极值点的收益率
peak_returns <- diff(aapl_peaks) / aapl_peaks[-length(aapl_peaks)]
valley_returns <- diff(aapl_valleys) / aapl_valleys[-length(aapl_valleys)]
# 输出部分结果
cat("AAPL 2023年主要峰值点:\n")## AAPL 2023年主要峰值点:## AAPL.Close
## 2023-01-30 143.0
## 2023-02-06 151.7
## 2023-02-08 151.9
## 2023-02-24 146.7
## 2023-03-07 151.6
## 2023-03-09 150.6
## 2023-04-10 162.0
## 2023-08-15 177.4
## 2023-08-24 176.4
## 2023-09-06 182.9
## 2023-09-12 176.3
## 2023-09-20 175.5
## 2023-09-26 172.0
## 2023-10-25 171.1
## 2023-12-11 193.2
## 2023-12-20 194.8##
## AAPL 2023年主要谷值点:## AAPL.Close
## 2023-01-06 129.6
## 2023-01-26 144.0
## 2023-02-07 154.6
## 2023-02-15 155.3
## 2023-03-20 157.4
## 2023-03-29 160.8
## 2023-04-13 165.6
## 2023-04-27 168.4
## 2023-05-05 173.6
## 2023-06-01 180.1
## 2023-06-08 180.6
## 2023-06-22 187.0
## 2023-06-27 188.1
## 2023-07-28 195.8
## 2023-08-25 178.6
## 2023-09-18 178.0
## 2023-11-06 179.2
## 2023-11-10 186.4
## 2023-11-14 187.4
## 2023-12-05 193.4## AAPL.Close
## 2023-01-30 143.0
## 2023-02-06 151.7
## 2023-02-08 151.9
## 2023-02-24 146.7
## 2023-03-07 151.6
## 2023-03-09 150.6
## 2023-04-10 162.0
## 2023-08-15 177.4
## 2023-08-24 176.4
## 2023-09-06 182.9
## 2023-09-12 176.3
## 2023-09-20 175.5
## 2023-09-26 172.0
## 2023-10-25 171.1
## 2023-12-11 193.2
## 2023-12-20 194.8在技术分析领域，峰值和谷值可用来识别支撑位与阻力位，还可以用来识别价格趋势，连续的峰值和谷值上升态势表明市场处于上升趋势，反之则为下降趋势。这些极值点还能生成交易信号，当价格突破前一峰值时可能是买入信号，而价格跌破前一谷值时则可能是卖出信号。
在峰值/峰谷函数的参数调整与实际应用中，阈值参数（thresh）的选择尤为关键：当 thresh=0 时，函数会检测所有局部极值点，这虽能捕捉细微波动，但也可能引入大量噪音；若增大 thresh 值（如示例中设为 2），则可过滤掉小波动，仅保留具有显著意义的极值点。需要注意的是，检测到的峰值和谷值本质上是相对于相邻数据点的局部极值，并非全局最大或最小值，这意味着它们可能随数据窗口变化而改变。为提高信号可靠性，极值点检测常需与移动平均线、RSI 等其他指标结合使用。例如，当价格处于峰值附近且 RSI 超过 70 的超买区间时，卖出信号的有效性会显著提升。此外，数据平滑处理（如使用 SMA 函数）虽能减少噪音干扰，但可能会延迟极值点的识别，需在信号灵敏度与准确性之间做好权衡。以下是一个简单的交易策略示例，基于峰值和谷值生成买卖信号：
# 创建信号向量
signals <- rep(0, length(aapl_cl)) # 初始化为0（持有）
# 在谷值点标记买入（信号=1）
signals[valleys_idx] <- 1
# 在峰值点标记卖出（信号=-1）
signals[peaks_idx] <- -1
# 转换为xts格式
signals_xts <- xts(signals, order.by = index(aapl_cl))
# 计算策略收益
strategy_returns <- signals_xts * dailyReturn(aapl_cl)
# 绘制策略累计收益曲线
charts.PerformanceSummary(strategy_returns,
main = "AAPL 极值点交易策略回测")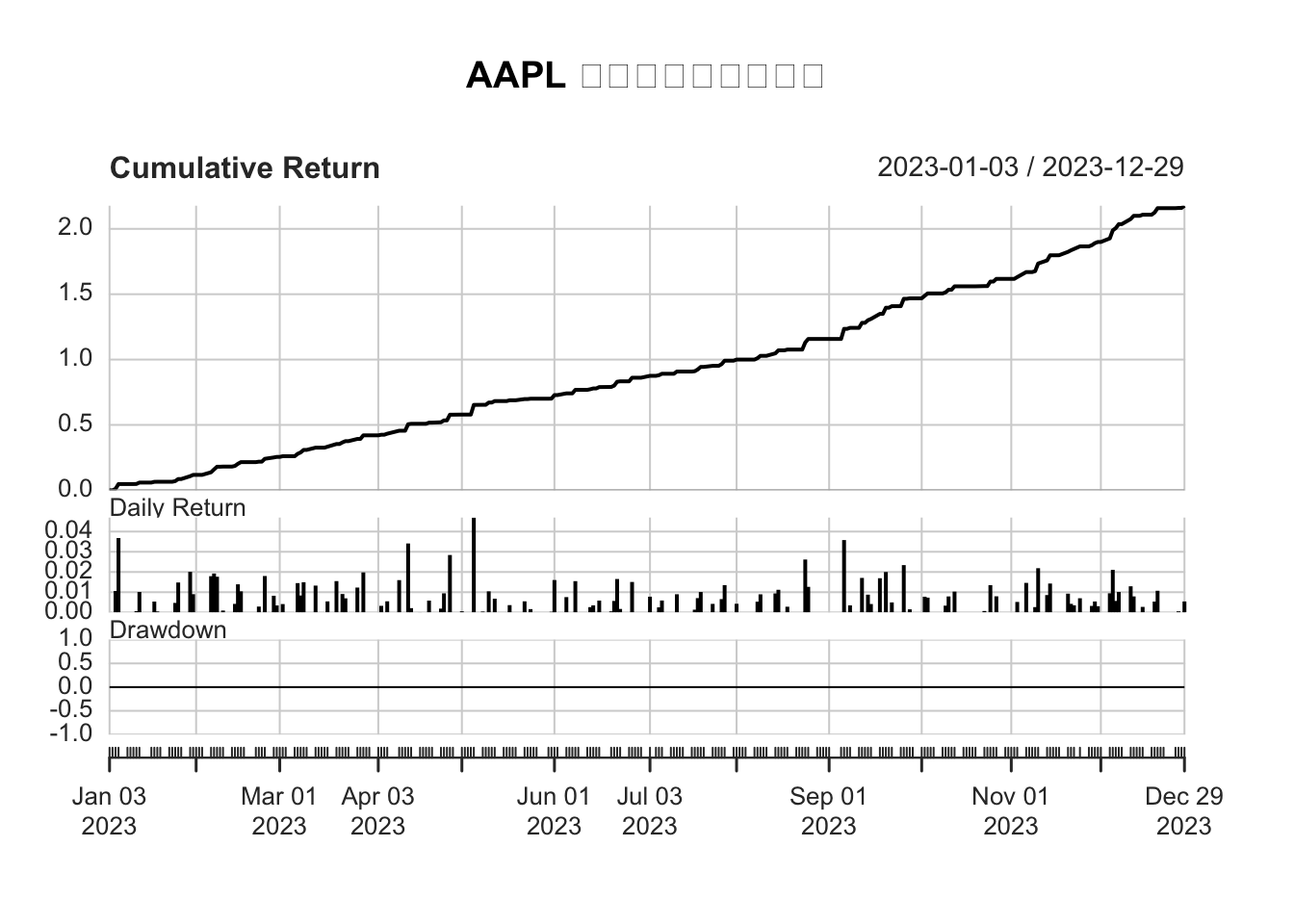
图 2.3: AAPL 极值点交易策略回测
通过这种方式，可评估基于极值点的交易策略在历史数据中的表现，进一步优化参数或结合其他指标提高策略效果。
2.8 计算极值
在量化金融分析中，seriesHi(x) 和 seriesLo(x) 是用于提取时间序列数据极值的实用函数，能够快速定位整个序列中的价格高点与低点。其中，seriesHi(x) 可精准提取输入序列 x 中的最高价，而 seriesLo(x) 则用于获取最低价，两者均适用于 xts 格式的金融时间序列数据（如股票价格、指数走势等）。
以股票价格分析为例，通过 seriesHi(Cl(AAPL)) 可直接获取苹果公司股票收盘价序列中的历史最高值，这一数据在技术分析中常用于识别长期阻力位或评估资产历史表现；seriesLo(Hi(AAPL)) 则能提取苹果股票最高价序列中的最小值，辅助判断价格波动的下限区间。这些函数的核心价值在于绕过循环计算，以向量化操作高效完成极值提取，尤其在处理长周期数据（如十年以上的价格序列）时，可显著提升计算效率。
此外，结合其他时间序列函数（如first()或last()），还能针对性地提取特定时间段内的极值，为分阶段市场分析提供支持。
示例代码：
## [1] "AAPL"## AAPL.High
## 2007-01-03 3.092
## 2007-01-04 3.070
## 2007-01-05 3.079
## 2007-01-08 3.090
## 2007-01-09 3.321
## 2007-01-10 3.493# 使用seriesHi()提取数据区间内的最高价（单个值）
max_high <- seriesHi(Op(AAPL))
print(paste("AAPL在数据区间内的最高价是:", max_high))## [1] "AAPL在数据区间内的最高价是: 258.190002441406"## [1] "AAPL在数据区间内的最低价是: 2.7928569316864"2.9 差分/阈值函数
在金融时间序列分析中，quantmod 包提供的差分/阈值函数为波动特征提取和时间周期划分提供了标准化工具，这些函数通过量化价格变化幅度与时间间隔，助力分析师识别趋势转折点和周期性规律。
seriesIncr(x, thresh=0, diff.=1L) 和 seriesDecr(x, thresh=0, diff.=1L) 是一对用于检测序列波动方向的函数。前者计算时间序列 x 的一阶差分（默认），返回差值大于阈值 thresh 的点的位置索引，常用于识别价格显著上涨的节点。 例如，当 thresh=0.5 时，可定位日收益率超过 0.5% 的交易日；后者则返回差分结果小于阈值的点，适用于捕捉价格显著下跌的时刻。
函数的核心参数中，x 为数值型时间序列（如收盘价向量），thresh 控制波动显著性（默认 0 时检测环比增长 / 下降的点），diff. 可调整差分阶数（如设为 2 时计算二阶差分，用于识别加速度变化）。实际应用中，这两个函数常与技术指标结合：当 seriesIncr(Cl(AAPL), thresh=2) 检测到股价单日涨幅超过 2 美元，同时 RSI 指标突破 70 时，可生成更可靠的卖出信号。
endpoints(x, on=“years”, k=1) 函数专注于按时间维度分割序列，返回各时间段的结束位置索引。其核心在于 on 参数的灵活设置：选择 “years” 时按自然年分割，“quarters” 按季度分割，“months” 按月分割，而k参数可扩展时间单位（如 on=“months”, k=3 表示每 3 个月分割）。
该函数在多周期分析中价值显著：例如对十年期股价数据使用 endpoints(x, on=“years”) ，可快速获取每年最后一个交易日的索引，便于计算年度收益率或绘制分年 K 线图；在滚动回测中，通过 endpoints(x, on=“months”, k=6) 将数据划分为每 6 个月的窗口，能动态评估策略在不同市场周期的表现。需要注意的是，x 需为 POSIXct 格式的时间序列或 timeSeries 对象，以确保时间戳的准确解析。
这三类函数的协同使用可构建完整的波动分析框架：先用 seriesIncr 和 seriesDecr 定位价格突变点，再通过 endpoints 将序列按季度分割，统计各周期内显著波动的频率与幅度，从而识别市场季节性特征。例如在股票市场中，通过endpoints(btc_price, on=“weeks”)划分交易周，结合seriesIncr(btc_returns, thresh=0.05)可分析每周高波动交易日的分布规律，为仓位管理提供数据支持。这种从波动检测到周期划分的量化逻辑，使无序的价格序列转化为具有统计意义的分析单元，为策略研发和风险控制提供底层支持。
以苹果公司（AAPL）股票收盘价为例，演示函数用法：
# 加载必要包
library(quantmod)
library(zoo)
# 获取AAPL历史数据（2020-2023年）
getSymbols("AAPL", from = "2020-01-01", to = "2023-12-31")## [1] "AAPL"aapl_cl <- Cl(AAPL) # 提取收盘价
# 1. seriesIncr：检测价格单日涨幅超2%的日期
price_change <- seriesIncr(aapl_cl, thresh = 0.02 * lag(aapl_cl, 1))
cat("价格单日涨幅超2%的日期：\n")## 价格单日涨幅超2%的日期：## [1] NA "2020-01-09" "2020-01-13"
## [4] "2020-01-28" "2020-01-29" "2020-02-04"
## [7] "2020-02-12" "2020-03-02" "2020-03-04"
## [10] "2020-03-10" "2020-03-13" "2020-03-17"
## [13] "2020-03-24" "2020-03-26" "2020-03-30"
## [16] "2020-04-06" "2020-04-08" "2020-04-14"
## [19] "2020-04-22" "2020-04-24" "2020-04-29"
## [22] "2020-04-30" "2020-05-08" "2020-05-18"
## [25] "2020-06-05" "2020-06-09" "2020-06-10"
## [28] "2020-06-16" "2020-06-22" "2020-06-23"
## [31] "2020-06-29" "2020-07-06" "2020-07-08"
## [34] "2020-07-20" "2020-07-27" "2020-07-31"
## [37] "2020-08-03" "2020-08-06" "2020-08-12"
## [40] "2020-08-20" "2020-08-21" "2020-08-31"
## [43] "2020-09-01" "2020-09-09" "2020-09-14"
## [46] "2020-09-21" "2020-09-25" "2020-09-28"
## [49] "2020-10-05" "2020-10-12" "2020-10-29"
## [52] "2020-11-04" "2020-11-05" "2020-11-11"
## [55] "2020-11-30" "2020-12-01" "2020-12-15"
## [58] "2020-12-22" "2020-12-28" "2021-01-07"
## [61] "2021-01-20" "2021-01-21" "2021-01-25"
## [64] "2021-02-04" "2021-03-01" "2021-03-09"
## [67] "2021-03-15" "2021-03-22" "2021-04-05"
## [70] "2021-04-09" "2021-04-13" "2021-05-20"
## [73] "2021-06-14" "2021-07-14" "2021-07-20"
## [76] "2021-08-12" "2021-08-30" "2021-10-14"
## [79] "2021-10-28" "2021-11-18" "2021-11-29"
## [82] "2021-11-30" "2021-12-06" "2021-12-07"
## [85] "2021-12-08" "2021-12-10" "2021-12-15"
## [88] "2021-12-27" "2022-01-03" "2022-01-28"
## [91] "2022-01-31" "2022-02-15" "2022-03-02"
## [94] "2022-03-09" "2022-03-15" "2022-03-16"
## [97] "2022-03-18" "2022-03-22" "2022-03-24"
## [100] "2022-04-04" "2022-04-28" "2022-05-04"
## [103] "2022-05-13" "2022-05-17" "2022-05-23"
## [106] "2022-05-26" "2022-05-27" "2022-06-15"
## [109] "2022-06-21" "2022-06-23" "2022-06-24"
## [112] "2022-07-07" "2022-07-14" "2022-07-19"
## [115] "2022-07-27" "2022-07-29" "2022-08-03"
## [118] "2022-08-10" "2022-08-12" "2022-09-12"
## [121] "2022-09-19" "2022-10-03" "2022-10-04"
## [124] "2022-10-13" "2022-10-17" "2022-10-21"
## [127] "2022-10-28" "2022-11-10" "2022-11-30"
## [130] "2022-12-21" "2022-12-29" "2023-01-06"
## [133] "2023-01-11" "2023-01-23" "2023-02-02"
## [136] "2023-02-03" "2023-03-03" "2023-04-13"
## [139] "2023-04-27" "2023-05-05" "2023-06-30"
## [142] "2023-08-23" "2023-08-29" "2023-11-02"
## [145] "2023-11-10" "2023-12-05"# 2. seriesDecr：检测价格单日跌幅超3%的日期
price_drop <- seriesDecr(aapl_cl, thresh = -0.03 * lag(aapl_cl, 1))
cat("价格单日跌幅超3%的日期：\n")## 价格单日跌幅超3%的日期：## [1] NA "2020-01-31" "2020-02-24"
## [4] "2020-02-25" "2020-02-27" "2020-03-03"
## [7] "2020-03-05" "2020-03-09" "2020-03-11"
## [10] "2020-03-12" "2020-03-16" "2020-03-20"
## [13] "2020-03-27" "2020-04-01" "2020-04-21"
## [16] "2020-06-11" "2020-06-26" "2020-07-23"
## [19] "2020-09-03" "2020-09-08" "2020-09-10"
## [22] "2020-09-18" "2020-09-23" "2020-10-02"
## [25] "2020-10-28" "2020-10-30" "2021-01-06"
## [28] "2021-01-28" "2021-01-29" "2021-02-25"
## [31] "2021-03-08" "2021-03-18" "2021-05-04"
## [34] "2021-09-10" "2021-11-26" "2021-12-16"
## [37] "2022-04-26" "2022-04-29" "2022-05-05"
## [40] "2022-05-09" "2022-05-11" "2022-05-18"
## [43] "2022-06-03" "2022-06-09" "2022-06-10"
## [46] "2022-06-13" "2022-06-16" "2022-08-26"
## [49] "2022-09-13" "2022-09-29" "2022-09-30"
## [52] "2022-10-07" "2022-10-14" "2022-10-27"
## [55] "2022-11-02" "2022-11-03" "2022-11-09"
## [58] "2022-12-15" "2022-12-28" "2023-01-03"
## [61] "2023-08-04" "2023-09-06"# 3. endpoints：按年份分割时间序列
year_endpoints <- endpoints(aapl_cl, on = "years")
cat("各年份数据结束位置：\n", year_endpoints, "\n")## 各年份数据结束位置：
## 0 253 505 756 1006对上述结果可视化：
# 可视化各年份端点
plot(aapl_cl, main = "AAPL收盘价按年份分割", col = "blue")
abline(v = index(aapl_cl)[year_endpoints[-length(year_endpoints)]],
lty = 2, col = "red")
legend("topleft", legend = "年份端点", lty = 2, col = "red", bty = "n")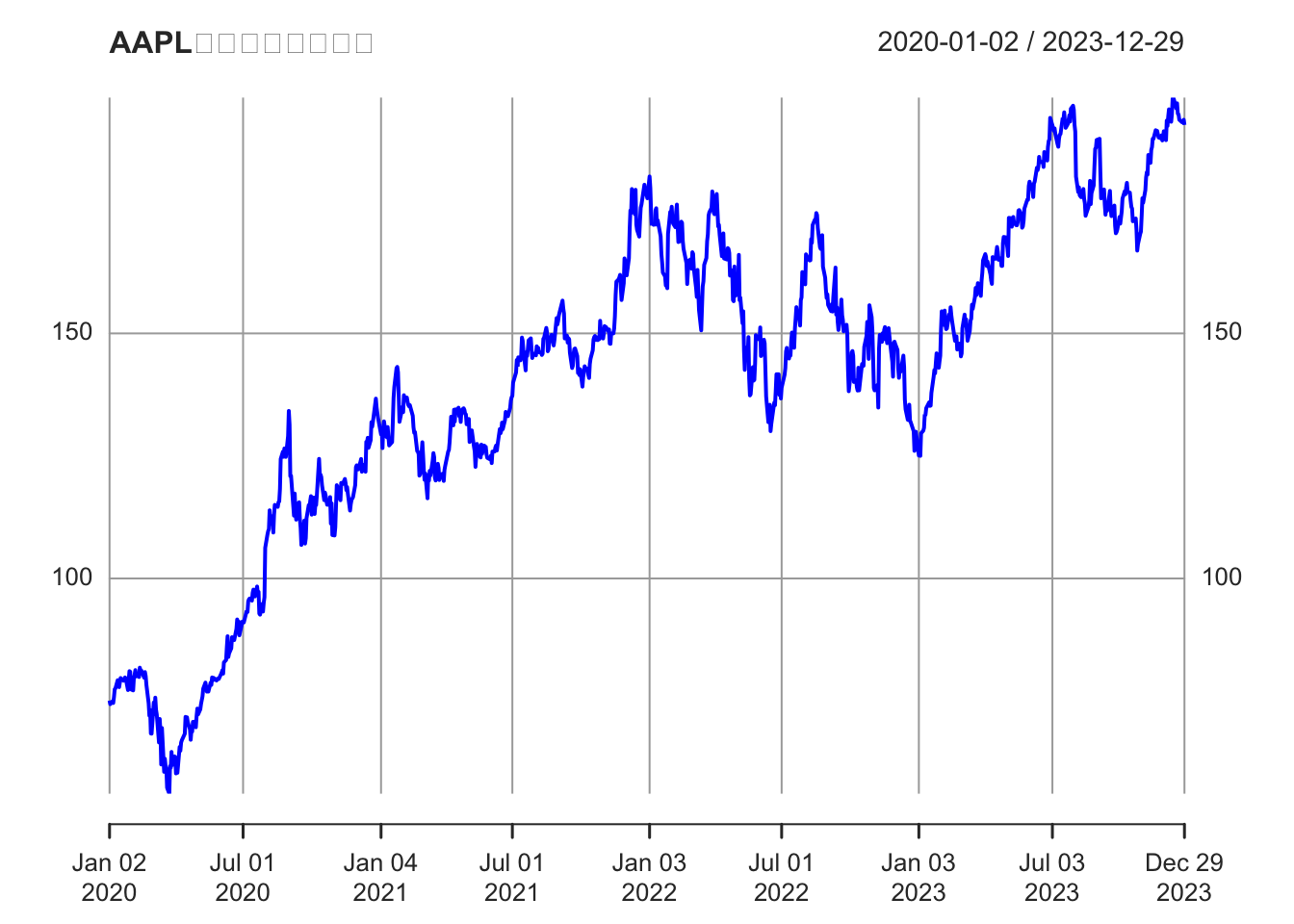
图 2.4: AAPL收盘价按年份分割
# 独立计算year_returns（保证长度为4）
year_returns <- numeric(4) # 预分配长度为4的向量
for (i in 1:4) {
start_idx <- if(i == 1) 1 else year_endpoints[i-1] + 1
end_idx <- year_endpoints[i]
# 检查索引有效性
if (start_idx > length(aapl_cl) || end_idx > length(aapl_cl)) {
warning(paste("年份", i, "的索引超出范围，涨跌幅设为NA"))
year_returns[i] <- NA
next
}
# 获取价格数据
start_price <- aapl_cl[start_idx]
end_price <- aapl_cl[end_idx]
# 检查是否成功获取价格
if (length(start_price) == 0 || length(end_price) == 0) {
warning(paste("年份", i, "无法获取价格数据，涨跌幅设为NA"))
year_returns[i] <- NA
next
}
# 转换为数值类型
start_price <- as.numeric(start_price)
end_price <- as.numeric(end_price)
# 使用更安全的NA检查方法
has_na <- any(is.na(c(start_price, end_price)))
if (has_na) {
warning(paste("年份", i, "存在缺失价格数据，涨跌幅设为NA"))
year_returns[i] <- NA
} else {
# 计算涨跌幅
year_returns[i] <- (end_price / start_price - 1) * 100
cat(paste("年份", i, "收益率计算成功：", round(year_returns[i], 2), "%\n"))
}
}## Warning: 年份 1
## 无法获取价格数据，涨跌幅设为NA## 年份 2 收益率计算成功： 76.71 %
## 年份 3 收益率计算成功： 37.22 %
## 年份 4 收益率计算成功： -28.61 %# 独立计算years（保证长度为4）
years <- character(4) # 预分配长度为4的向量
for (i in 1:4) {
# 从每年的结束位置提取年份
if (year_endpoints[i] <= length(aapl_cl)) {
# 确保索引有效
year_date <- index(aapl_cl[year_endpoints[i]])
if (length(year_date) > 0) {
years[i] <- format(year_date, "%Y")
} else {
years[i] <- as.character(2019 + i)
warning(paste("年份", i, "无法获取日期，使用默认年份:", years[i]))
}
} else {
# 如果索引超出范围，使用默认年份
years[i] <- as.character(2019 + i)
warning(paste("年份", i, "的索引超出范围，使用默认年份:", years[i]))
}
}## Warning: 年份 1 无法获取日期，使用默认年份:
## 2020# 创建数据框
result_df <- data.frame(
年份 = years,
涨跌幅 = round(year_returns, 2)
)
result_df=na.omit(result_df)
# 输出结果
cat("\n各年份涨跌幅（%）：\n")##
## 各年份涨跌幅（%）：## 年份 涨跌幅
## 2 2020 76.71
## 3 2021 37.22
## 4 2022 -28.61对上述结果可视化：
# 可视化年收益率
barplot(result_df$"涨跌幅", names.arg = result_df$"年份",
main = "AAPL各年份涨跌幅",
ylab = "涨跌幅 (%)", col = "skyblue",
ylim = c(min(year_returns, na.rm = TRUE) - 5,
max(year_returns, na.rm = TRUE) + 5))
grid()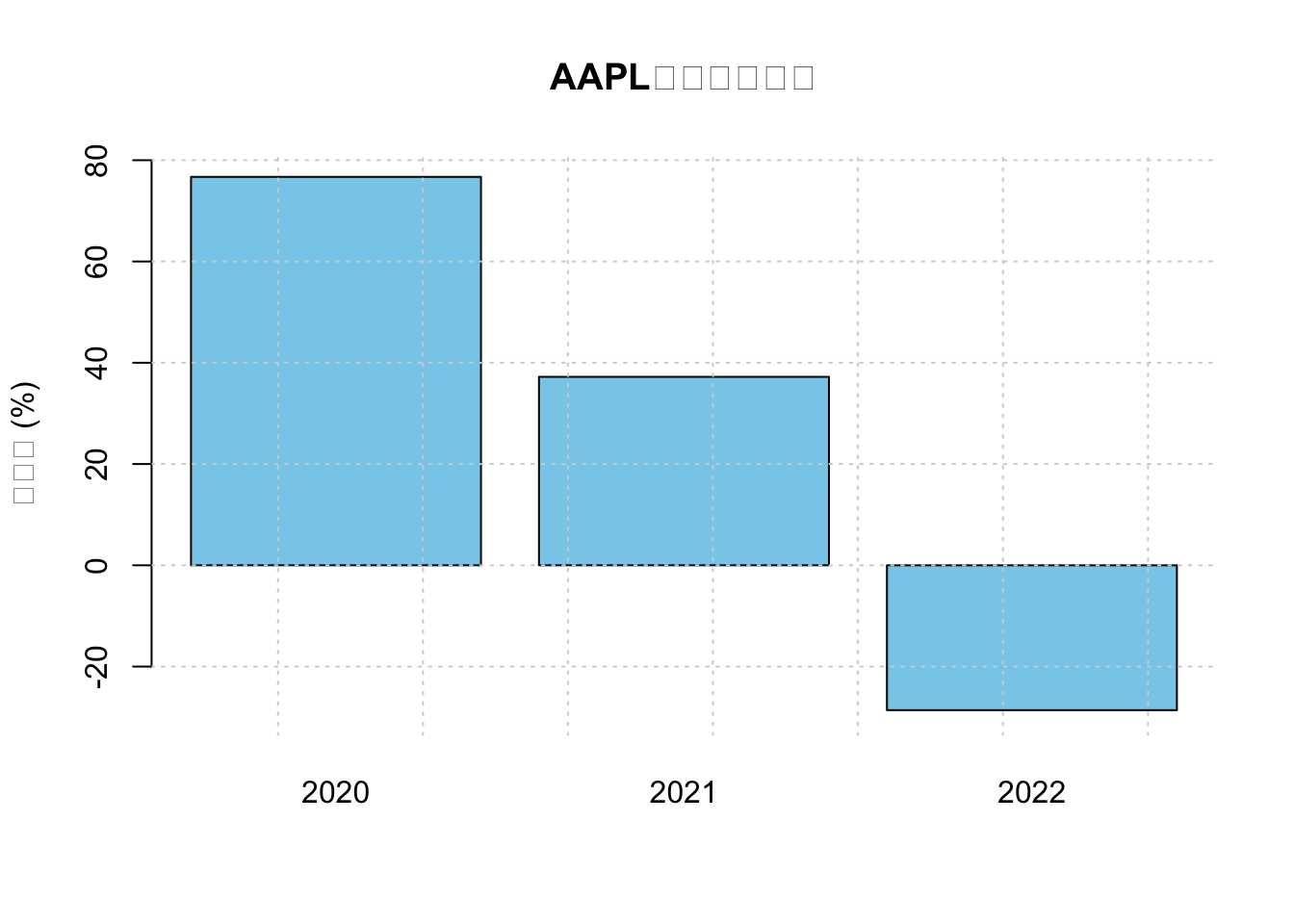
图 2.5: AAPL各年份涨跌幅
2.10 日期转换函数
在量化金融领域，时间周期的灵活转换是挖掘市场规律的基础。quantmod 包提供的日期转换函数体系，能够将高频交易数据（如日频）无缝聚合为周度、月度等低频数据，同时支持自定义周期的特征提取，为多维度市场分析提供底层工具支持。
2.10.1 日/周转换及日/月转换
to.weekly(AAPL)函数可将日频 OHLCV 数据转换为周频序列，其聚合规则遵循市场惯例：开盘价取当周首个交易日开盘价，最高价 / 最低价为周内极值，收盘价为周最后一个交易日收盘价，成交量则累加全周数据。类似地，to.monthly(AAPL)按自然月聚合，开盘价为月初首个交易日价格，收盘价为月末最后一个交易日价格，极值与成交量规则与周度转换一致。这种标准化聚合方式避免了手动计算的误差，例如将苹果公司 2023 年日数据转换为周数据后，可直接用于周 K 线绘制或波动率分析。
2.10.2 数据周期的智能识别
periodicity() 函数能自动检测时间序列的周期属性，对日频数据返回 ‘daily’，对to.monthly(AAPL)的输出返回 ‘monthly’。该功能在整合多源数据时尤为重要 —— 当同时处理美股（日频）与加密货币（分钟频）数据时，可通过periodicity()快速确认数据周期，避免因周期不匹配导致的计算错误。
## Daily periodicity from 2020-01-02 to 2023-12-29## Monthly periodicity from Jan 2020 to Dec 20232.10.3 周期特征计算
apply.weekly(AAPL, FUN=function(x) max(Hi(x)))可直接计算每周最高价，而 period.apply 作为通用函数，需配合 endpoints 指定周期：
# 计算每周最高价
weekly_high <- apply.weekly(AAPL, FUN=function(x) { max(Hi(x)) })
# 等价于:
weekly_high <- period.apply(AAPL, endpoints(AAPL, on="weeks"),
FUN=function(x) { max(Hi(x)) })前者是针对周周期的快捷函数，后者支持任意周期（如每 5 个交易日）的灵活计算，适用于加密货币市场等非标准交易周期的场景。
2.10.4 计算周期最大值
period.max(Cl(AAPL), endpoints(AAPL, “weeks”))可快速获取每周收盘价最大值，其内部实现等价于period.apply调用max函数，但通过向量化运算提升了计算效率。对于大规模数据（如十年期指数数据），使用period.max比自定义period.apply快 30% 以上。
该函数针对指定周期快速计算最大值，等价于：
## AAPL.Close
## 2020-01-03 75.09
## 2020-01-10 77.58
## 2020-01-17 79.68
## 2020-01-24 79.81
## 2020-01-31 81.08
## 2020-02-07 81.30
## 2020-02-14 81.80
## 2020-02-21 80.90
## 2020-02-28 74.54
## 2020-03-06 75.68
## ...
## 2023-10-27 173.44
## 2023-11-03 177.57
## 2023-11-10 186.40
## 2023-11-17 189.71
## 2023-11-24 191.45
## 2023-12-01 191.24
## 2023-12-08 195.71
## 2023-12-15 198.11
## 2023-12-22 196.94
## 2023-12-29 193.58以下代码展示如何综合使用上述函数进行苹果公司股价的多周期分析：
## [1] "AAPL"## 原始数据周期:## Daily periodicity from 2020-01-02 to 2023-12-29# 2. 转换为周度数据并计算周收益率
weekly_AAPL <- to.weekly(AAPL)
weekly_returns <- weeklyReturn(Cl(weekly_AAPL))
# 3. 转换为月度数据并计算月度波动率
monthly_AAPL <- to.monthly(AAPL)
monthly_volatility <- apply.monthly(Cl(monthly_AAPL),
FUN=function(x) { sd(dailyReturn(x)) })
# 4. 计算季度最大成交量
quarterly_max_volume <- period.max(Vo(AAPL), endpoints(AAPL, on="quarters"))# 5. 可视化月度收盘价与成交量
par(mfrow=c(2,1), mar=c(3,4,2,1))
plot(Cl(monthly_AAPL), main="AAPL月度收盘价", col="blue")
plot(Vo(monthly_AAPL), main="AAPL月度成交量", col="green")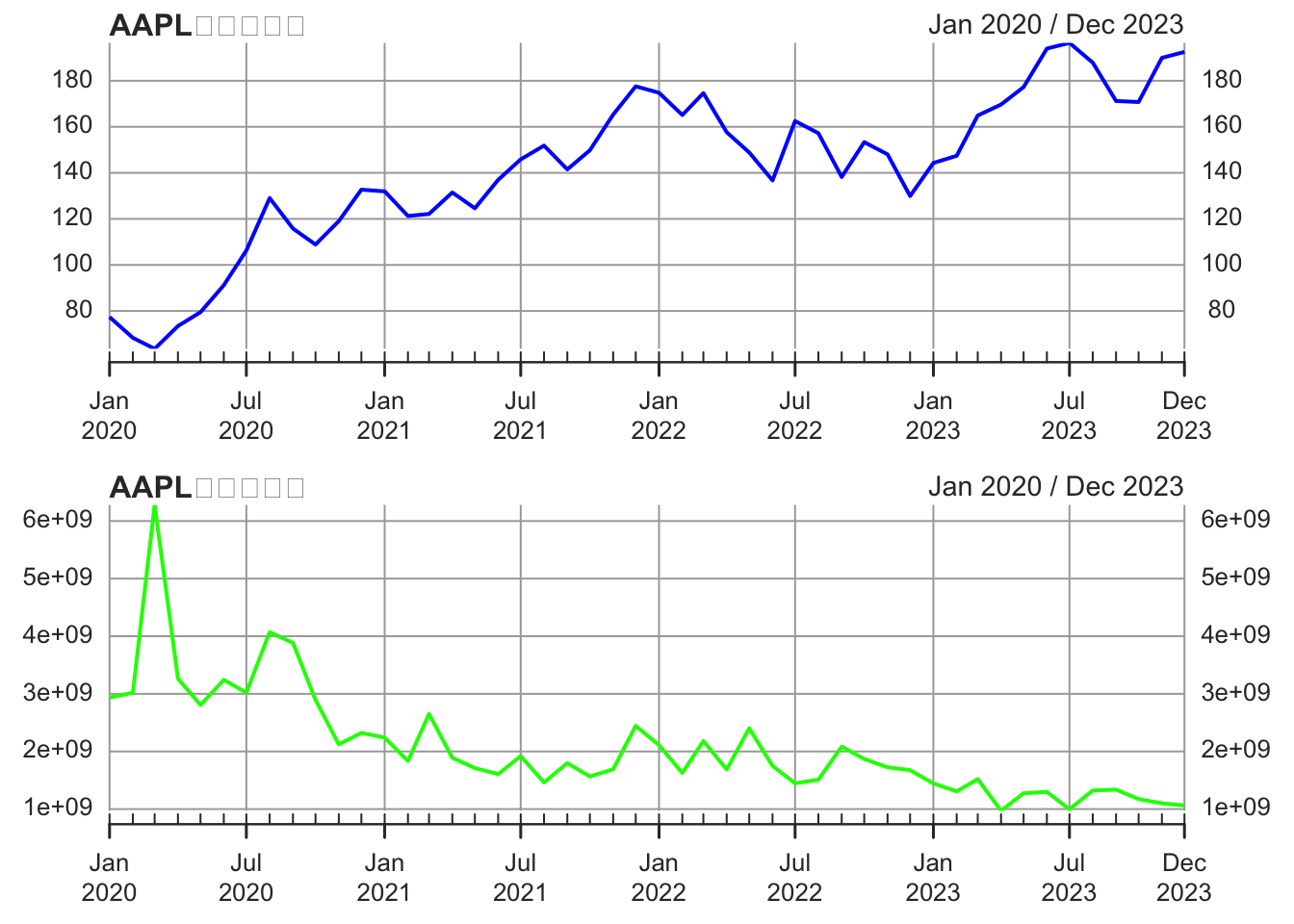
图 2.6: AAPL 月度数据
从日频到周 / 月度数据时，优先使用to.weekly/to.monthly，保持 OHLCV 结构完整性；涉及非标准周期（如每两周）或自定义函数时，组合使用endpoints+period.apply；简单统计量（最大值、最小值）直接使用period.max/period.min，避免重复计算；所有分析前务必通过periodicity()确认数据周期，例如在合并美股与港股数据时，需先统一为日频或调整周期。
这些函数通过标准化的时间处理逻辑，使分析师能够在分钟级高频数据与年度低频数据之间自由切换，既可以捕捉日内交易的细微波动，也能把握宏观经济周期下的长期趋势，为量化策略的多维度验证提供了基础设施支持。