第 4 章 时间序列分析中的 ARIMA 模型
4.1 如何平滑时间序列?
在 R 语言中,可以使用多种方法平滑时间序列,以下为你介绍常见的几种:
移动平均法(Moving Average)
移动平均是一种简单的平滑方法,通过计算一定时间窗口内数据的平均值来平滑序列。
- 简单移动平均(Simple Moving Average, SMA)
原理:对时间序列数据的一个固定长度窗口内的数据求平均。例如,对于时间序列 \(y_1,y_2,\cdots,y_n\) ,窗口大小为 \(k\) ,简单移动平均序列 \(SMA_t\) 的计算为 \(SMA_t=\frac{y_{t - \lfloor\frac{k - 1}{2}\rfloor}+\cdots + y_{t+\lfloor\frac{k - 1}{2}\rfloor}}{k}\) ,其中 \(t\) 为时间点,\(\lfloor\cdot\rfloor\) 为向下取整函数。
# 创建一个简单的时间序列
ts_data <- ts(c(12, 15, 18, 20, 22, 25, 27, 30), frequency = 1)
# 使用 stats 包中的 filter 函数实现简单移动平均,窗口大小为3
smoothed_data <- filter(ts_data, filter = rep(1/3, 3), sides = 1)
plot(ts_data, main = "Original vs Smoothed Time Series", ylab = "Value")
lines(smoothed_data, col = "red")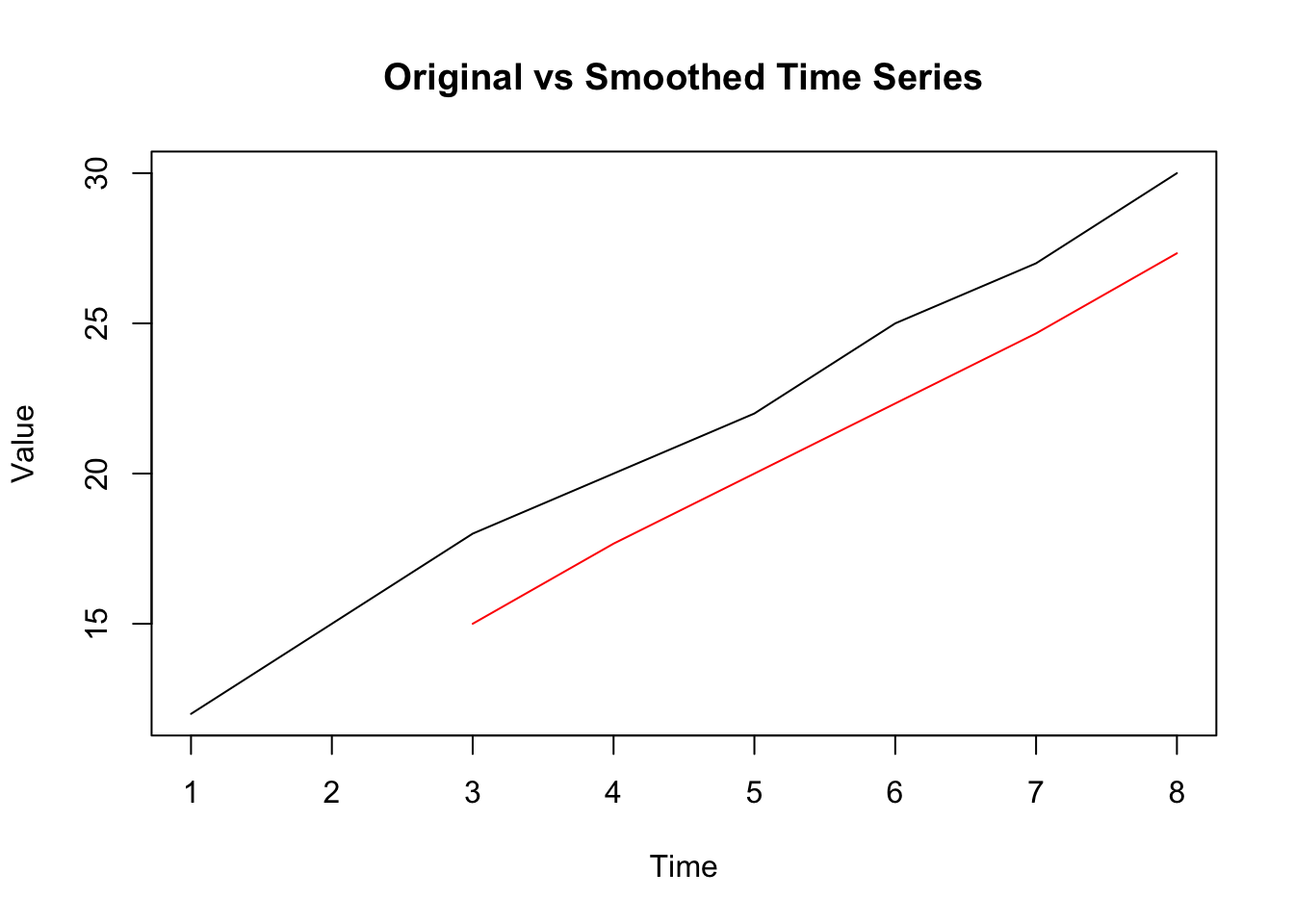
filter 函数中,filter 参数指定权重,这里使用等权重(窗口大小为 3 时,每个权重为 1/3),sides = 1 表示使用单边移动平均(即从序列开始依次计算移动平均)。
- 加权移动平均(Weighted Moving Average, WMA)
与简单移动平均类似,但窗口内的数据点赋予不同的权重,权重之和为 1。权重通常根据时间点与当前点的距离或其他重要性因素确定。
# 创建时间序列
ts_data <- ts(c(12, 15, 18, 20, 22, 25, 27, 30), frequency = 1)
# 定义权重,这里使用递减权重
weights <- c(0.1, 0.3, 0.6)
weighted_smoothed <- filter(ts_data, filter = weights, sides = 1)
plot(ts_data, main = "Original vs Weighted Smoothed Time Series", ylab = "Value")
lines(weighted_smoothed, col = "red")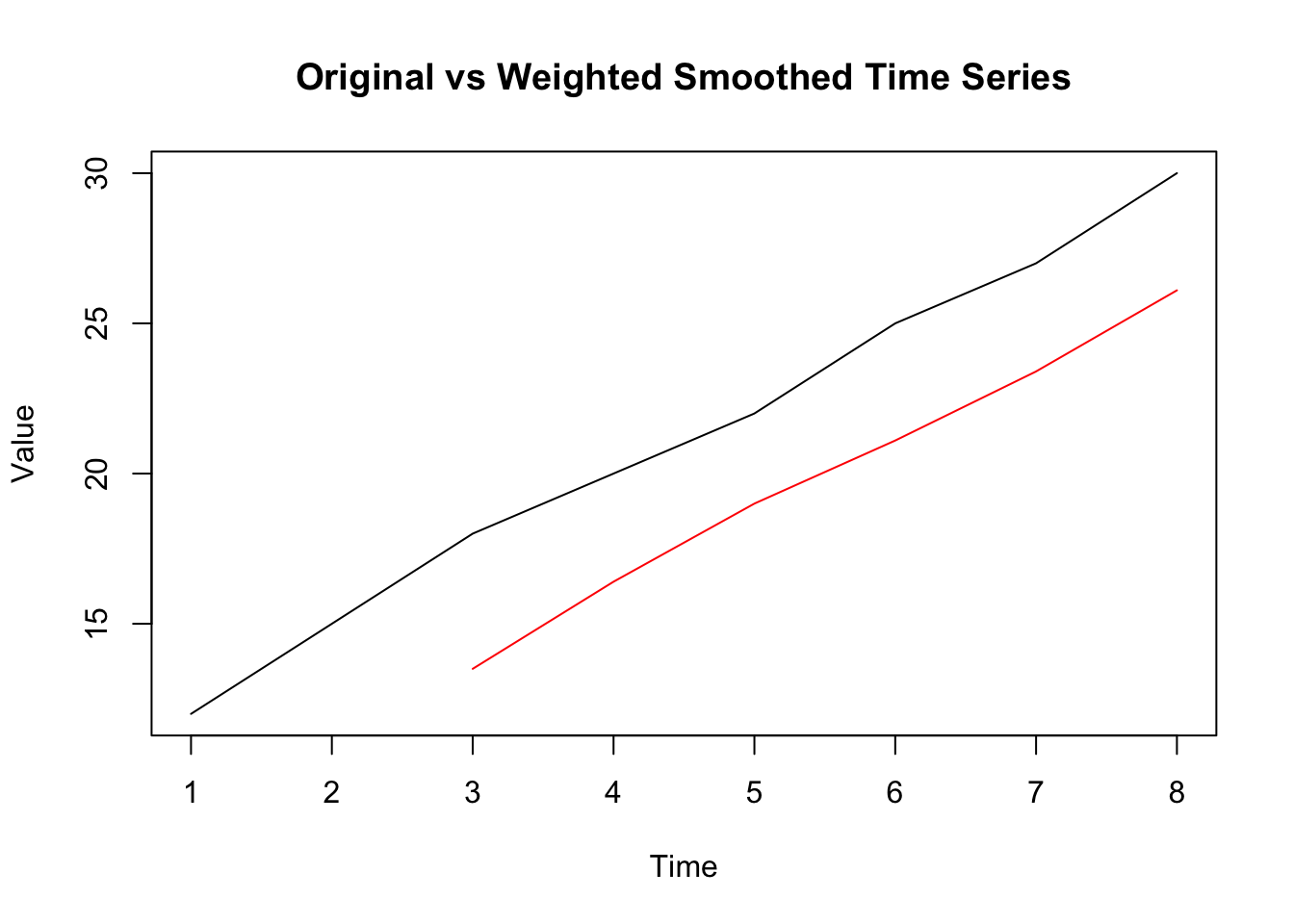
这里定义了权重weights,距离当前点越近的数据权重越大,然后使用filter函数计算加权移动平均。
- 指数平滑法(Exponential Smoothing)
指数平滑法对近期数据赋予更高的权重,对远期数据权重呈指数递减。
简单指数平滑(Simple Exponential Smoothing, SES)原理:
假设时间序列 \(y_t\) ,预测值 \(F_{t+1}\) 是当前实际值 \(y_t\) 和上一期预测值 \(F_t\) 的加权平均,即:
\[ F_{t + 1}=\alpha y_t+(1 - \alpha)F_t \]
其中: \(\alpha\) 是平滑参数,且 \(0<\alpha<1\) 。
## Registered S3 method overwritten by 'quantmod':
## method from
## as.zoo.data.frame zoots_data <- ts(c(12, 15, 18, 20, 22, 25, 27, 30), frequency = 1)
# 使用 ses 函数进行简单指数平滑,设置初始值和参数
fit <- ses(ts_data, alpha = 0.3, initial = "simple")
smoothed <- fitted(fit)
plot(ts_data, main = "Original vs SES Smoothed Time Series", ylab = "Value")
lines(smoothed, col = "red")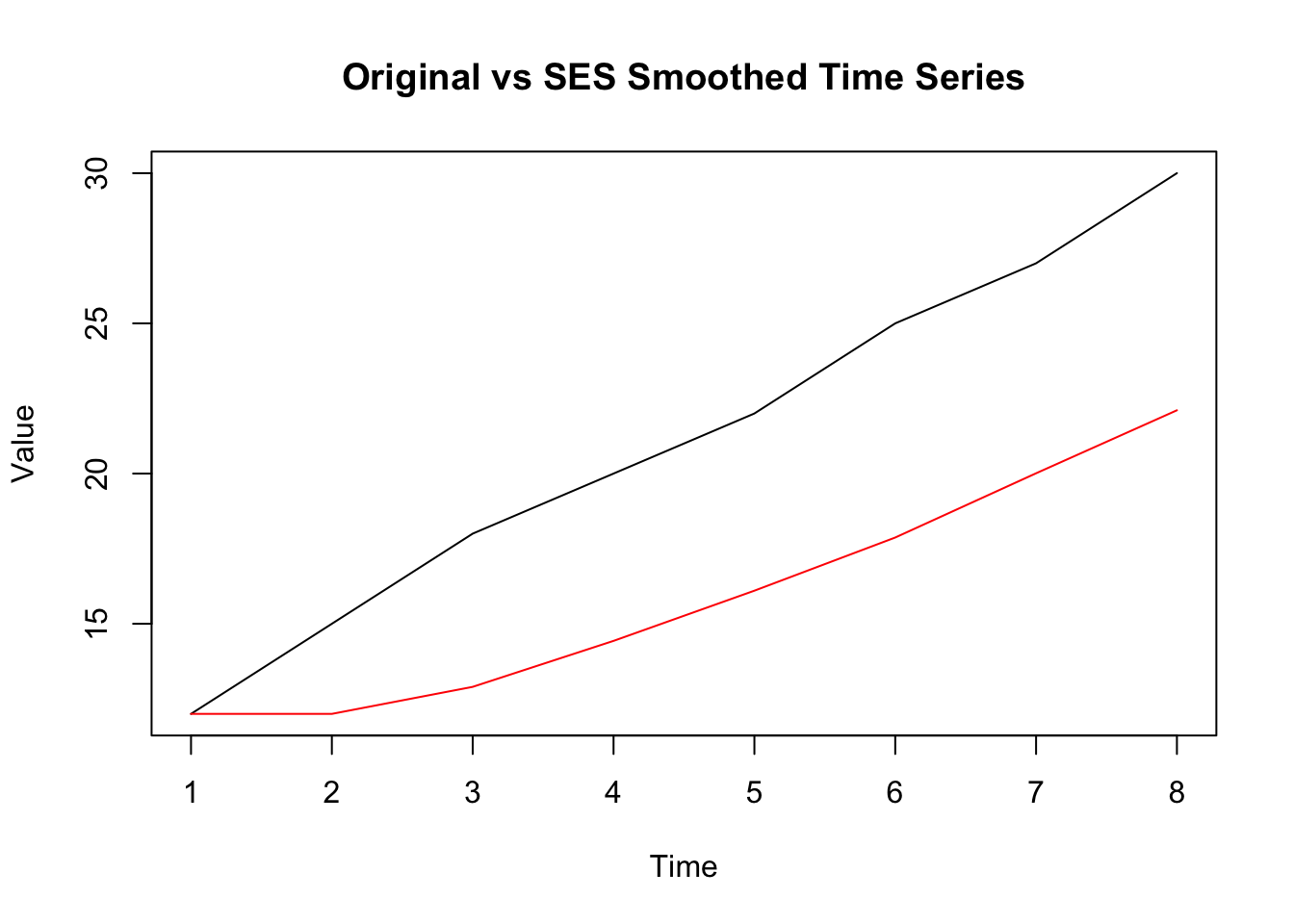
ses 函数来自forecast 包,alpha设置平滑参数,initial设置初始预测值的计算方法。
- Holt-Winters 指数平滑
用于处理具有趋势和季节性的时间序列。它有三个平滑参数 \(\alpha\)(水平平滑参数)、 \(\beta\) (趋势平滑参数)和 \(\gamma\)(季节性平滑参数),分别对时间序列的水平、趋势和季节性成分进行平滑。
library(forecast)
# 创建具有季节性的时间序列
ts_data <- ts(c(12, 15, 18, 20, 22, 25, 27, 30), frequency = 4)
fit <- HoltWinters(ts_data)
smoothed <- fitted(fit)
# 确保长度一致
if (length(smoothed) > length(ts_data)) {
smoothed <- smoothed[1:length(ts_data)]
}
plot(ts_data, main = "Original vs Holt - Winters Smoothed Time Series", ylab = "Value")
lines(smoothed, col = "red")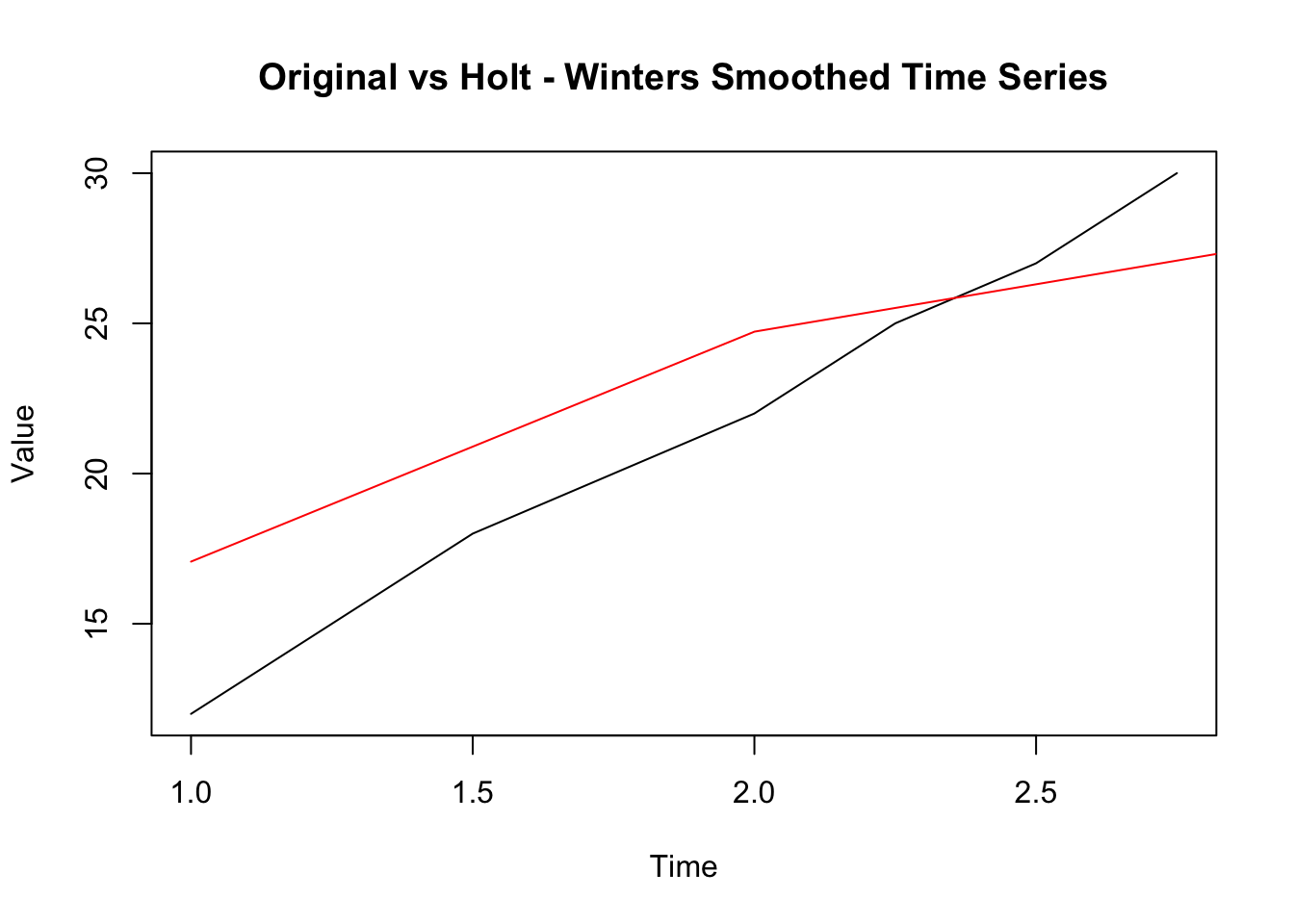
HoltWinters函数会自动估计平滑参数(也可手动设置),frequency参数指定季节性周期。
- 局部加权回归(Locally Weighted Scatterplot Smoothing, LOESS)
对每个数据点,在其局部邻域内拟合一个加权回归模型。权重通常基于数据点与目标点的距离确定,距离越近权重越高。
ts_data <- ts(c(12, 15, 18, 20, 22, 25, 27, 30), frequency = 1)
# 使用 loess 函数进行平滑
loess_fit <- loess(as.numeric(ts_data) ~ time(ts_data))
smoothed <- predict(loess_fit)
plot(ts_data, main = "Original vs LOESS Smoothed Time Series", ylab = "Value")
lines(smoothed, col = "red")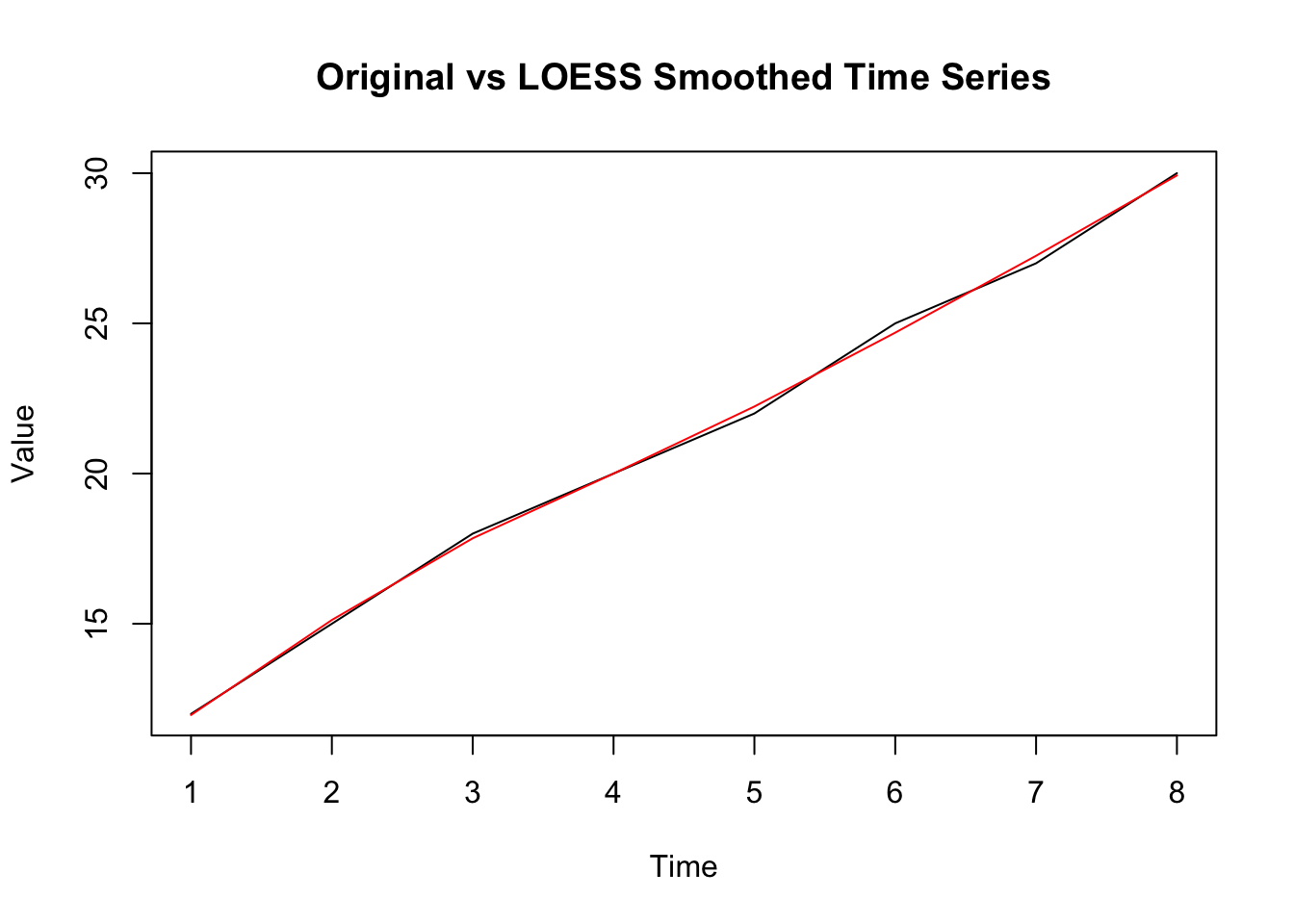
loess函数中,as.numeric(ts_data) ~ time(ts_data)表示对时间序列值与时间进行局部加权回归,predict函数获取平滑后的预测值。
这些方法各有特点,你可以根据时间序列的特征(如是否有趋势、季节性等)选择合适的平滑方法。
4.2 如何拟合 AR 模型
在金融时间序列分析中,使用 R 语言拟合自回归(AR)模型通常使用 stats 包,它是 R 语言的基础包,默认安装且加载,无需额外安装。如果需要进行更高级的时间序列分析和预测,还可以加载 forecast 包。
假设已经有一个金融时间序列数据,例如股票价格序列,将其转换为 R 语言中的时间序列对象。
# 示例数据,假设这是一个简单的价格序列
price_data <- c(100, 102, 105, 103, 107, 104, 109, 106, 110, 108)
# 将数据转换为时间序列对象
ts_data <- ts(price_data, frequency = 1)可以使用 ar 函数(来自 stats 包)或 auto.arima 函数(来自 forecast 包,它可以自动选择合适的 ARIMA 模型阶数,包括 AR 部分)来拟合 AR 模型。
使用 ar 函数
ar 函数通过不同的方法估计 AR 模型的参数,常用的方法有 yule - walker、burg 等。
# 使用 yule - walker 方法拟合 AR 模型,假设我们预先知道 AR 阶数为2
fit_ar <- ar(ts_data, order.max = 2, method = "yule-walker")
# 查看拟合结果
print(fit_ar)##
## Call:
## ar(x = ts_data, order.max = 2, method = "yule-walker")
##
##
## Order selected 0 sigma^2 estimated as 10.3在上述代码中:
order.max 参数指定了最大的 AR 阶数。这里设置为 2,表示拟合 AR (2) 模型。
method 参数指定估计方法,"yule - walker" 是一种常用的估计自回归模型参数的方法。
使用 auto.arima 函数
auto.arima 函数会自动选择合适的 ARIMA (p,d,q) 模型阶数,其中 p 是 AR 阶数。
# 使用 auto.arima 函数拟合 ARIMA 模型(会自动选择 AR 阶数)
fit_auto_arima <- auto.arima(ts_data)
# 查看拟合结果
print(fit_auto_arima)## Series: ts_data
## ARIMA(1,1,0) with drift
##
## Coefficients:
## ar1 drift
## -0.902 0.994
## s.e. 0.098 0.219
##
## sigma^2 = 1.8: log likelihood = -15.11
## AIC=36.22 AICc=41.02 BIC=36.81拟合模型后,需要对模型进行诊断,检查模型是否合适。常用的方法是查看残差的自相关函数(ACF)和偏自相关函数(PACF),理想情况下,残差应该是白噪声序列。
# 提取残差
residuals_ar <- residuals(fit_ar)
# 绘制残差的 ACF 和 PACF
par(mfrow = c(2,1))
acf(residuals_ar, main = "ACF of Residuals (AR Model)")
pacf(residuals_ar, main = "PACF of Residuals (AR Model)")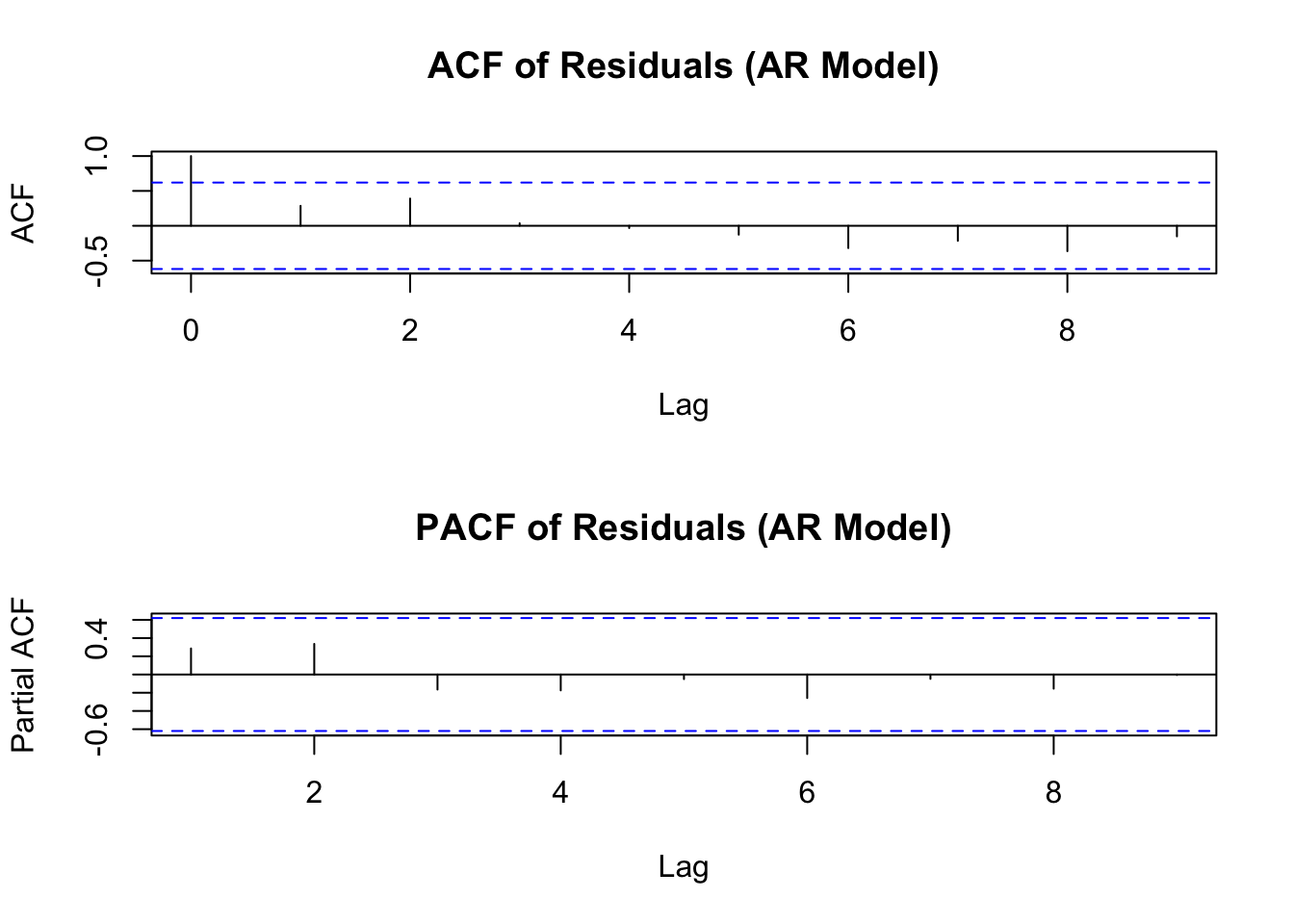
在上述代码中:
residuals 函数用于提取模型的残差。acf 和 pacf 函数分别用于绘制自相关函数和偏自相关函数图,通过观察这些图,可以判断残差是否为白噪声序列。如果残差是白噪声,ACF 和 PACF 图应该在零值附近随机波动,没有明显的模式。
4.3 如何使用拟合好的模型进行预测?
使用 ar 函数的预测
## $pred
## Time Series:
## Start = 11
## End = 13
## Frequency = 1
## [1] 105.4 105.4 105.4
##
## $se
## Time Series:
## Start = 11
## End = 13
## Frequency = 1
## [1] 3.204 3.204 3.204使用 auto.arima 函数的预测
# 使用拟合好的 auto.arima 模型进行预测,预测未来3期
forecast_auto_arima <- forecast(fit_auto_arima, h = 3)
# 查看预测结果
print(forecast_auto_arima)## Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
## 11 111.7 110.0 113.4 109.1 114.3
## 12 110.3 108.5 112.0 107.6 112.9
## 13 113.4 111.1 115.8 109.9 117.0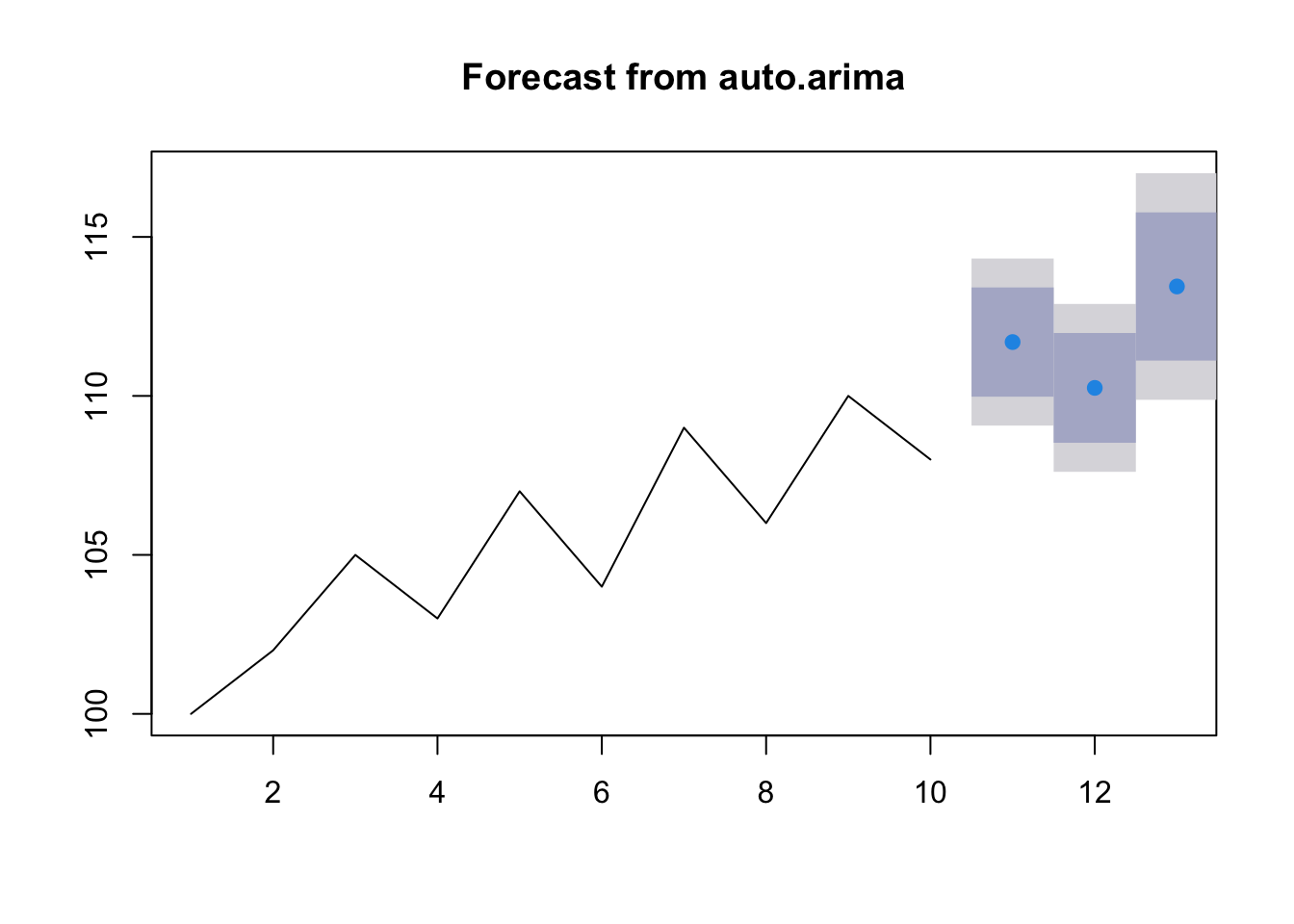
在上述代码中: predict 函数(用于 ar 模型的预测)和 forecast 函数(用于 auto.arima 模型的预测)的 n.ahead 或 h 参数指定了预测的期数。
通过以上步骤,可以在 R 语言中完成金融时间序列的 AR 模型拟合、诊断和预测。需要注意的是,在实际应用中,需要根据数据的特点和分析目的选择合适的方法和模型阶数。
4.4 如何拟合MA模型?
在 R 语言中拟合移动平均(MA)模型与拟合 AR 模型类似,通常使用基础的 stats 包,若需更高级的时间序列分析功能,可加载 forecast 包。
将金融时间序列数据转换为 R 语言中的时间序列对象。
# 示例数据,假设这是一个简单的收益率序列
return_data <- c(0.01, 0.02, -0.01, 0.03, -0.02, 0.04, 0.01, -0.03, 0.02, 0.05)
# 将数据转换为时间序列对象
ts_data <- ts(return_data, frequency = 1) 使用airma拟合模型
arima 函数可用于拟合 ARIMA (p, d, q) 模型,当 p = 0 时即为 MA (q) 模型。
##
## Call:
## arima(x = ts_data, order = c(0, 0, 1))
##
## Coefficients:
## ma1 intercept
## -1.000 0.009
## s.e. 0.259 0.002
##
## sigma^2 estimated as 0.000253: log likelihood = 26.02, aic = -46.04在上述代码中:order 参数设定了 ARIMA 模型的阶数,c(0, 0, 1) 分别对应 p(自回归阶数)、d(差分阶数)和 q(移动平均阶数),这里 p = 0,d = 0,q = 1 表示拟合 MA (1) 模型。
使用auto.arima 函数拟合模型
auto.arima 函数会自动选择合适的 ARIMA (p, d, q) 模型阶数,可能会选择到 MA 模型。
# 使用auto.arima函数拟合ARIMA模型(可能选择到MA模型)
fit_auto_arima <- auto.arima(ts_data)
# 查看拟合结果
print(fit_auto_arima) ## Series: ts_data
## ARIMA(0,0,0) with zero mean
##
## sigma^2 = 0.00074: log likelihood = 21.85
## AIC=-41.71 AICc=-41.21 BIC=-41.41拟合模型后需对其进行诊断,检查模型是否合适。同样可查看残差的自相关函数(ACF)和偏自相关函数(PACF),理想情况下,残差应是白噪声序列。
# 提取残差
residuals_ma <- residuals(fit_ma)
# 绘制残差的ACF和PACF
par(mfrow = c(2, 1))
acf(residuals_ma, main = "ACF of Residuals (MA Model)")
pacf(residuals_ma, main = "PACF of Residuals (MA Model)") 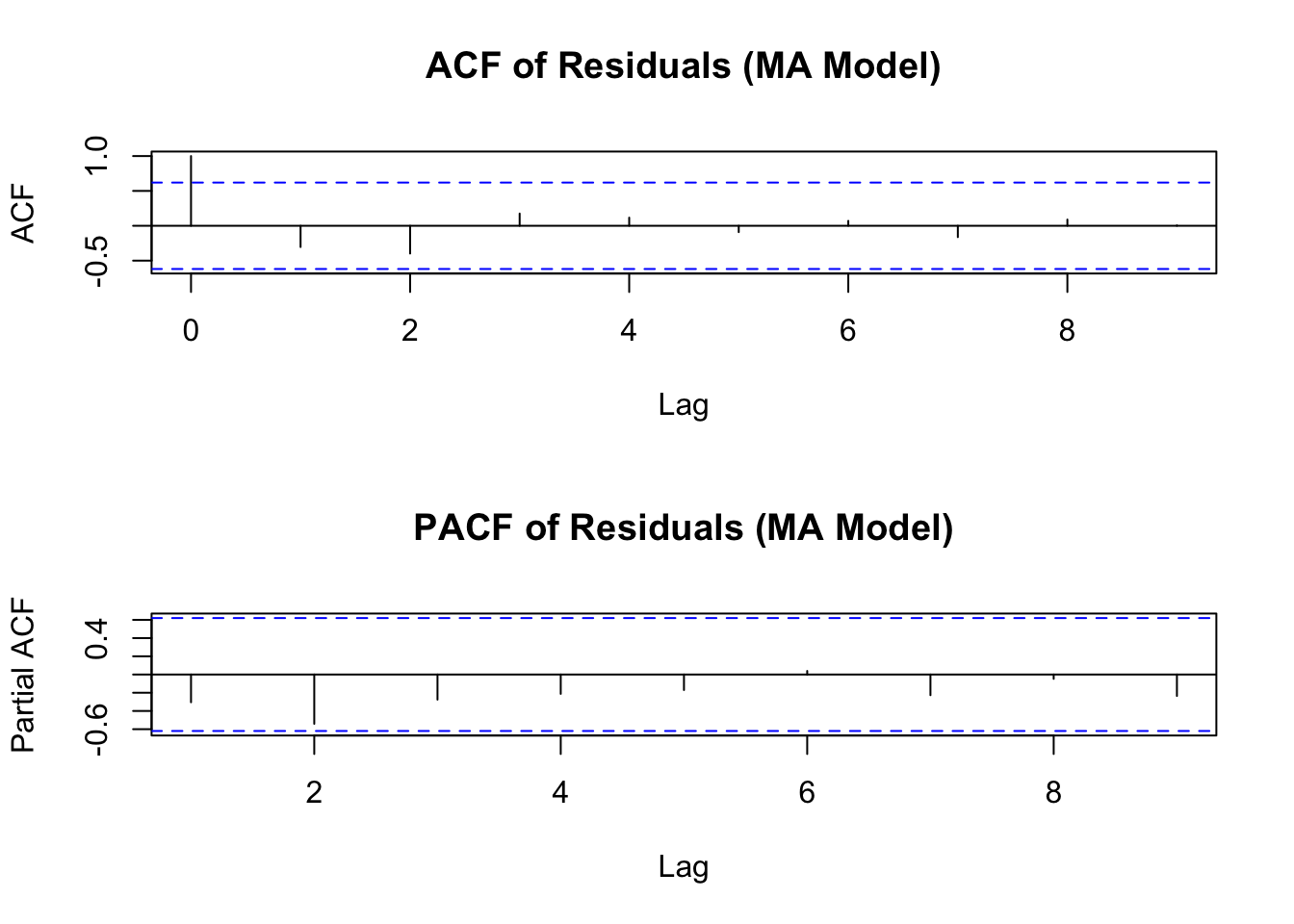
使用拟合好的模型进行预测。
使用 arima 函数的预测
## $pred
## Time Series:
## Start = 11
## End = 13
## Frequency = 1
## [1] -0.015092 0.009454 0.009454
##
## $se
## Time Series:
## Start = 11
## End = 13
## Frequency = 1
## [1] 0.01662 0.02250 0.02250使用 auto.arima 函数的预测
# 使用拟合好的auto.arima模型进行预测,预测未来3期
forecast_auto_arima <- forecast(fit_auto_arima, h = 3)
# 查看预测结果
print(forecast_auto_arima) ## Point Forecast Lo 80 Hi 80 Lo 95
## 11 0 -0.03486 0.03486 -0.05332
## 12 0 -0.03486 0.03486 -0.05332
## 13 0 -0.03486 0.03486 -0.05332
## Hi 95
## 11 0.05332
## 12 0.05332
## 13 0.05332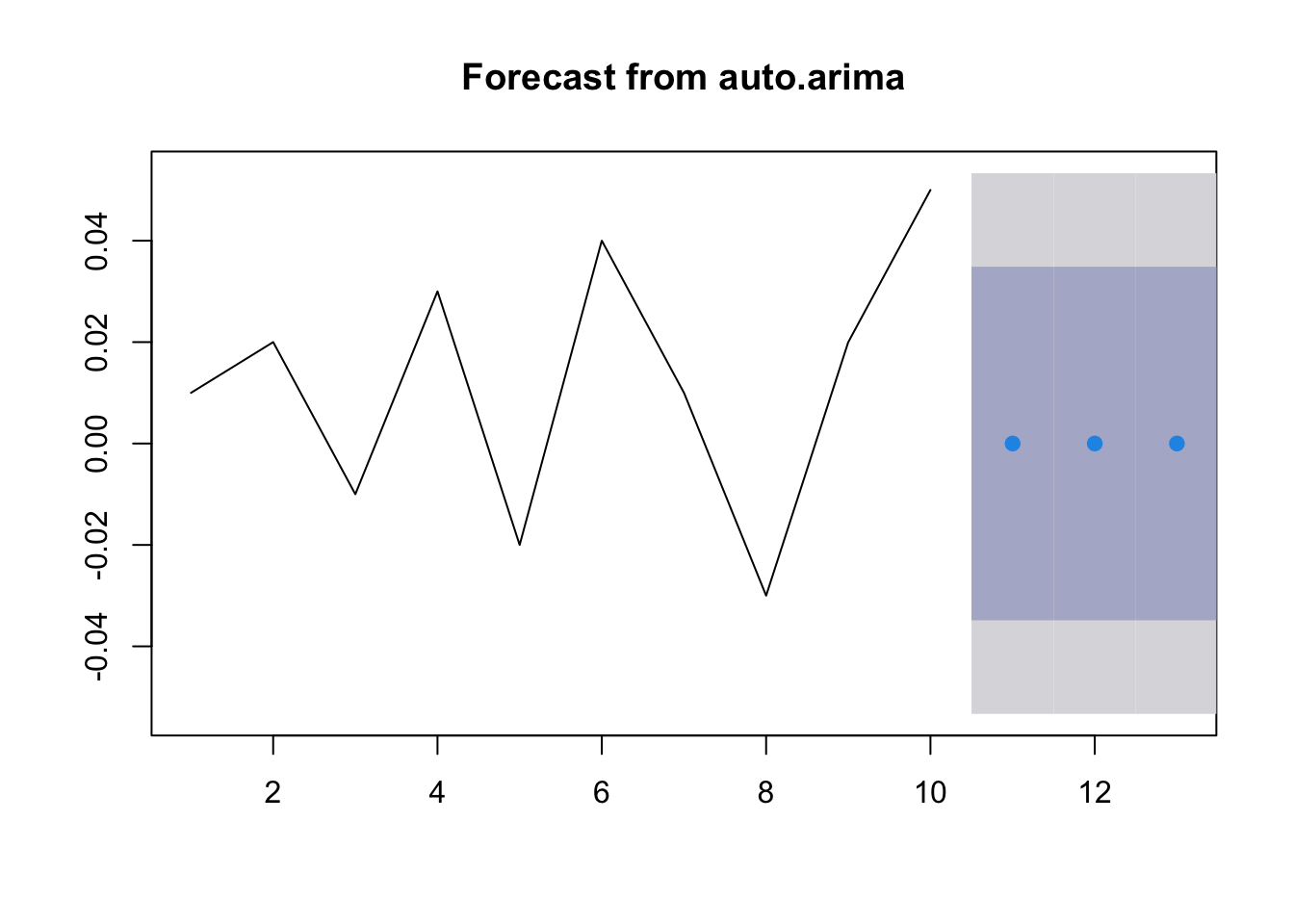
在预测部分,predict 函数(用于 arima 模型的预测)和 forecast 函数(用于 auto.arima 模型的预测)的 n.ahead 或 h 参数指定了预测的期数。
4.5 如何拟合 ARIMA 模型?
在 R 语言中拟合自回归积分滑动平均(ARIMA)模型,通常会用到 stats 包,它是 R 语言的基础包,默认已安装并加载。若需要更高级的时间序列分析和预测功能,还可以加载 forecast 包。
假设已有金融时间序列数据,需将其转换为 R 语言中的时间序列对象。
# 示例数据,假设这是一个简单的股价序列
stock_price <- c(100, 102, 105, 103, 107, 104, 109, 106, 110, 108)
# 将数据转换为时间序列对象
ts_data <- ts(stock_price, frequency = 1) ARIMA 模型要求数据是平稳的,或者通过差分使其平稳。可以通过绘制时间序列图、计算自相关函数(ACF)和偏自相关函数(PACF),或者使用单位根检验(如 ADF 检验)来判断数据的平稳性。
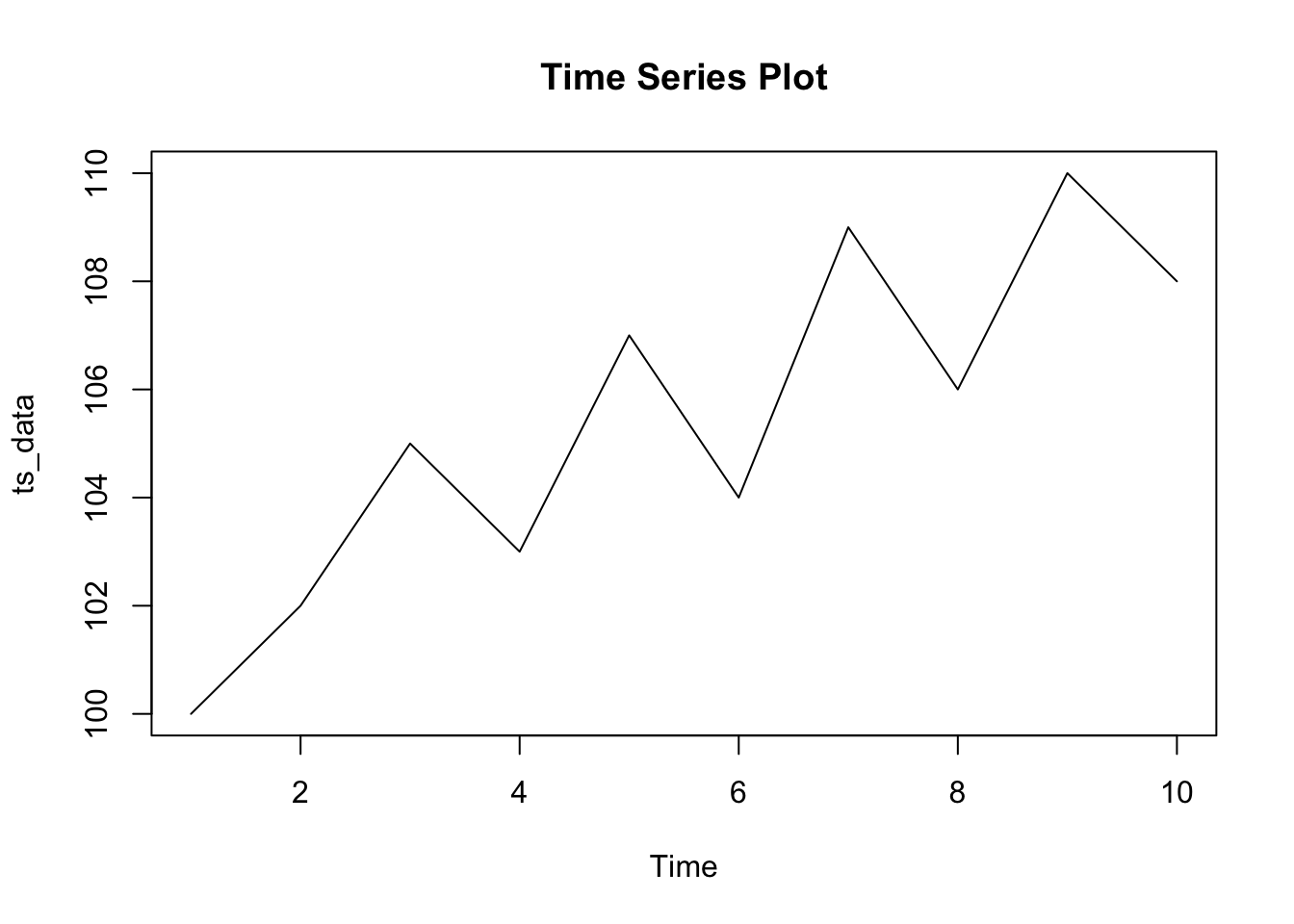
# 计算ACF和PACF
par(mfrow = c(2,1))
acf(ts_data, main = "ACF of Time Series")
pacf(ts_data, main = "PACF of Time Series")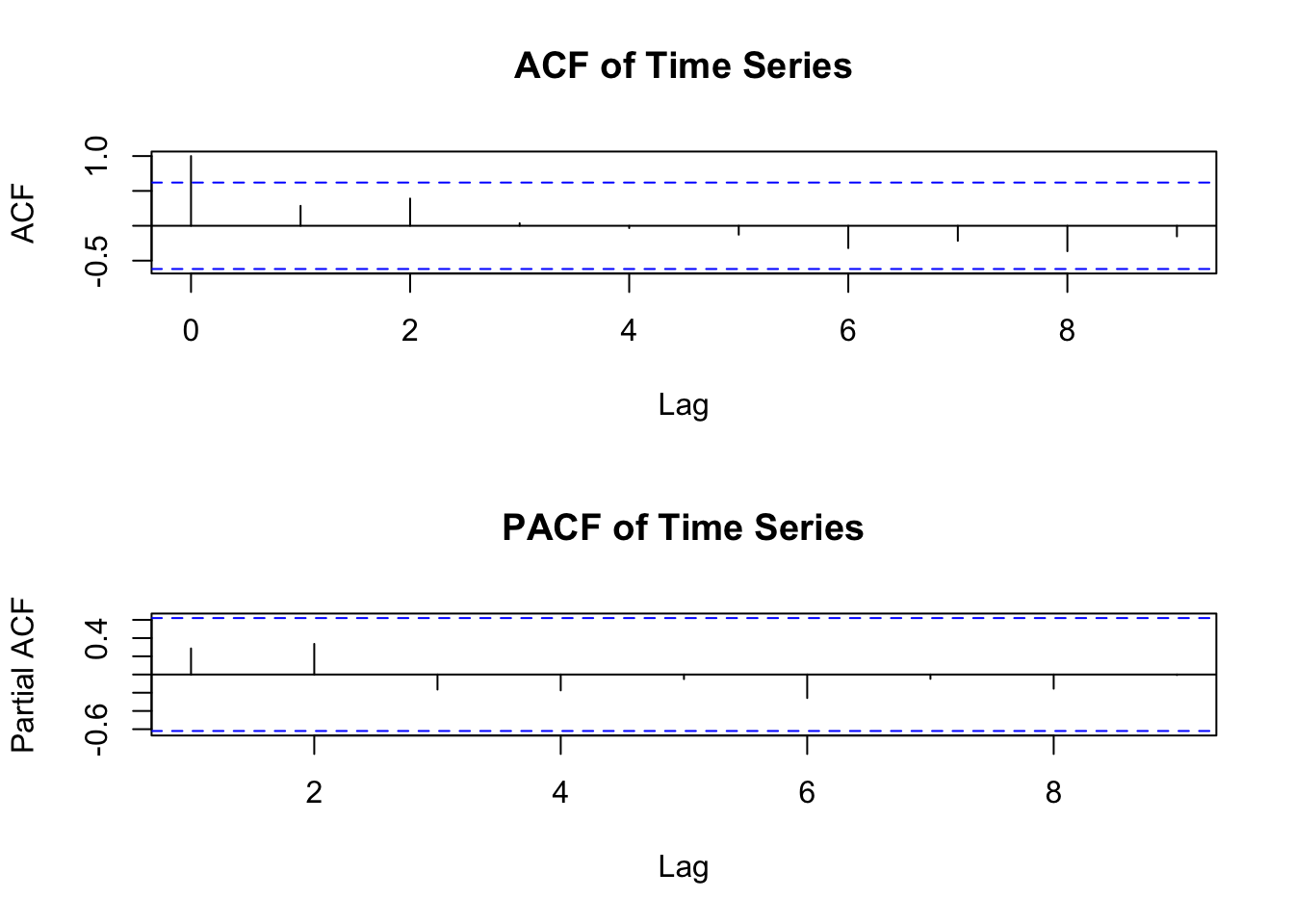
##
## Augmented Dickey-Fuller Test
##
## data: ts_data
## Dickey-Fuller = -2.2, Lag order = 2, p-value
## = 0.5
## alternative hypothesis: stationary如果数据不平稳,通常需要进行差分处理。d 表示差分阶数,例如一阶差分可以这样实现:
使用 arima 函数手动指定阶数 arima 函数可用于拟合 ARIMA (p, d, q) 模型,其中 p 是自回归阶数,d 是差分阶数,q 是移动平均阶数。你需要根据数据的 ACF 和 PACF 图,以及经验来选择合适的 p、d 和 q 值。
# 假设经过分析,选择p = 1, d = 1, q = 1
fit_arima <- arima(ts_data, order = c(1, 1, 1))
# 查看拟合结果
print(fit_arima) ##
## Call:
## arima(x = ts_data, order = c(1, 1, 1))
##
## Coefficients:
## ar1 ma1
## -0.866 0.340
## s.e. 0.172 0.361
##
## sigma^2 estimated as 4.09: log likelihood = -19.51, aic = 45.03使用 auto.arima 函数自动选择阶数 auto.arima 函数(来自 forecast 包)可以自动选择合适的 ARIMA 模型阶数。它会尝试不同的 p、d、q 组合,并根据信息准则(如 AIC、BIC 等)选择最优模型。
## Series: ts_data
## ARIMA(1,1,0) with drift
##
## Coefficients:
## ar1 drift
## -0.902 0.994
## s.e. 0.098 0.219
##
## sigma^2 = 1.8: log likelihood = -15.11
## AIC=36.22 AICc=41.02 BIC=36.81拟合模型后,需要对模型进行诊断,以确保模型合适。主要通过检查残差是否为白噪声序列来判断。
# 提取残差
residuals_arima <- residuals(fit_arima)
# 绘制残差的ACF和PACF
par(mfrow = c(2,1))
acf(residuals_arima, main = "ACF of Residuals")
pacf(residuals_arima, main = "PACF of Residuals")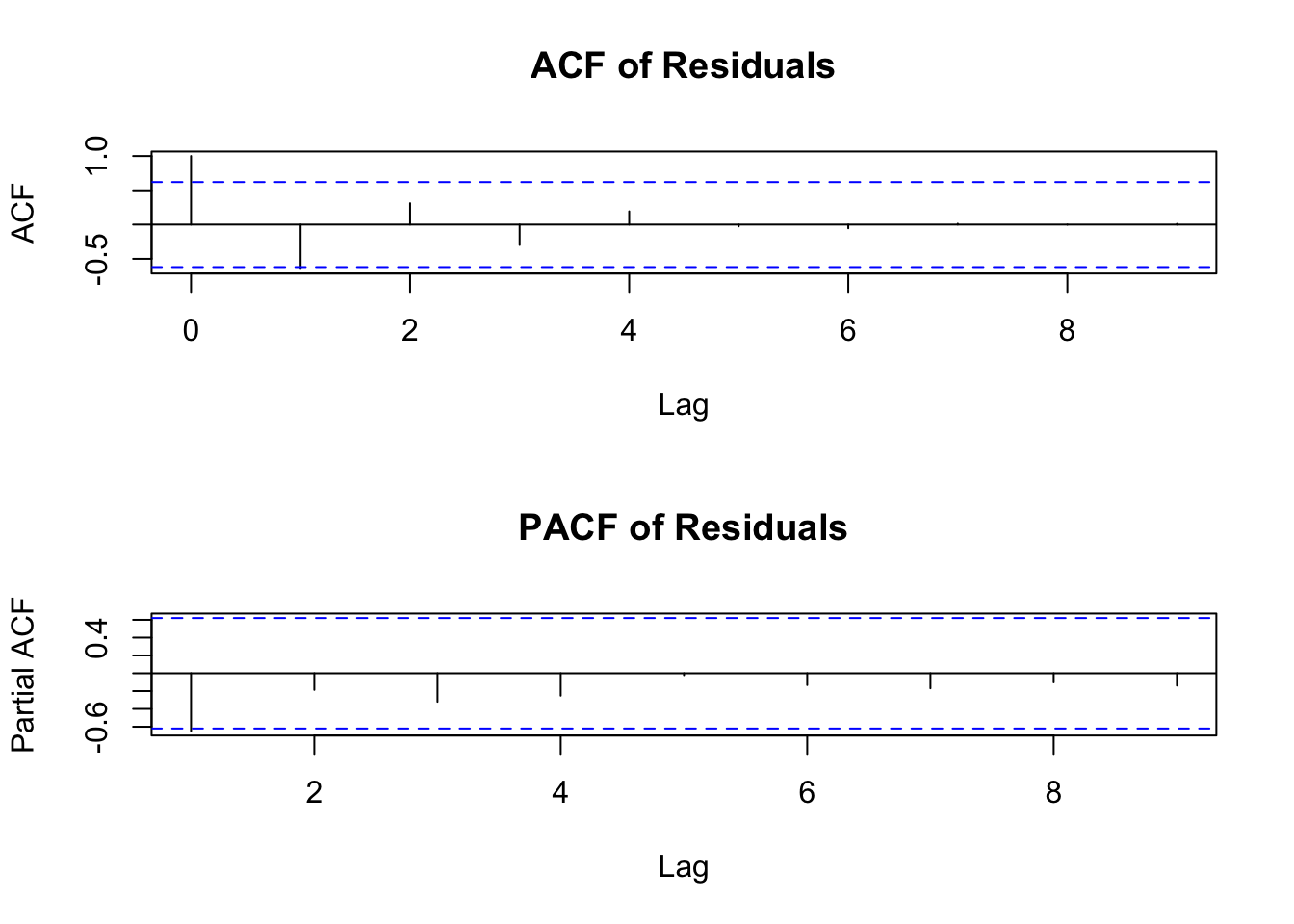
##
## Box-Ljung test
##
## data: residuals_arima
## X-squared = NA, df = 10, p-value = NA理想情况下,残差的 ACF 和 PACF 应在零值附近随机波动,Ljung - Box 检验的 p 值应大于显著性水平(如 0.05),表明残差是白噪声序列,即模型已充分捕捉数据中的信息。
使用拟合好的 ARIMA 模型进行预测。
使用 arima 函数的预测
# 使用拟合好的ARIMA模型进行预测,预测未来3期
forecast_arima <- predict(fit_arima, n.ahead = 3)
# 查看预测结果
print(forecast_arima) ## $pred
## Time Series:
## Start = 11
## End = 13
## Frequency = 1
## [1] 110.1 108.3 109.8
##
## $se
## Time Series:
## Start = 11
## End = 13
## Frequency = 1
## [1] 2.022 2.238 2.923使用 auto.arima 函数的预测
# 使用拟合好的auto.arima模型进行预测,预测未来3期
forecast_auto_arima <- forecast(fit_auto_arima, h = 3)
# 查看预测结果
print(forecast_auto_arima) ## Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
## 11 111.7 110.0 113.4 109.1 114.3
## 12 110.3 108.5 112.0 107.6 112.9
## 13 113.4 111.1 115.8 109.9 117.0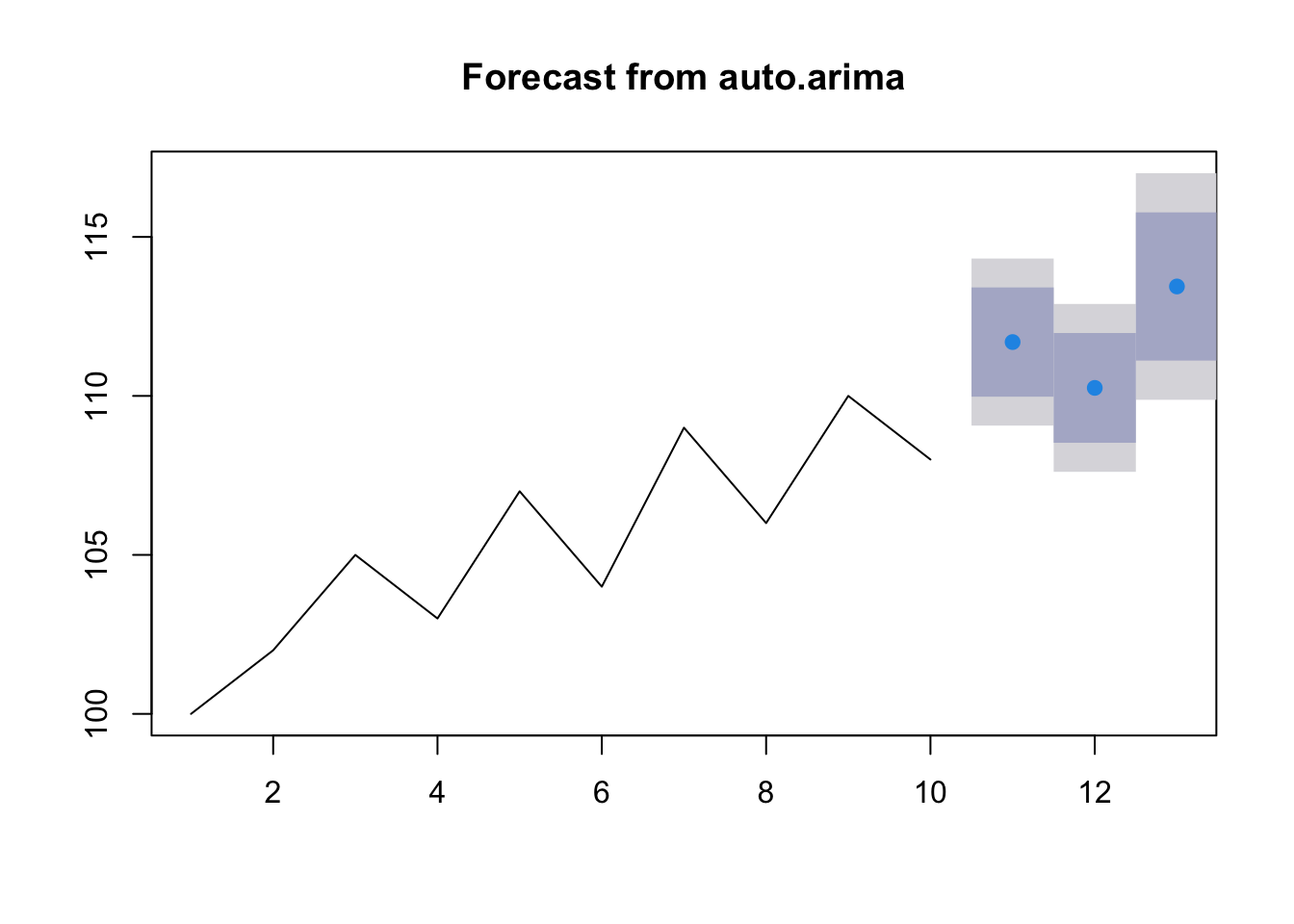
在预测部分,predict 函数(用于 arima 模型的预测)和 forecast 函数(用于 auto.arima 模型的预测)的 n.ahead 或 h 参数指定了预测的期数。
4.6 如何拟合 VAR 模型?
在 R 语言中拟合向量自回归(VAR)模型,常用的是 vars 包,它提供了一系列用于 VAR 模型估计、检验和预测的函数。
选择合适的滞后阶数对 VAR 模型很关键。可以使用信息准则,如赤池信息准则(AIC)、贝叶斯信息准则(BIC)等来确定。
# 使用 VARselect 函数来选择滞后阶数
lag_selection <- VARselect(Canada, lag.max = 5, type = "const")
print(lag_selection)## $selection
## AIC(n) HQ(n) SC(n) FPE(n)
## 3 2 2 3
##
## $criteria
## 1 2 3 4
## AIC(n) -5.817852 -6.350937 -6.397756 -6.145942
## HQ(n) -5.577530 -5.918357 -5.772918 -5.328846
## SC(n) -5.217992 -5.271189 -4.838120 -4.106417
## FPE(n) 0.002976 0.001752 0.001686 0.002202
## 5
## AIC(n) -5.926500
## HQ(n) -4.917146
## SC(n) -3.407087
## FPE(n) 0.002811在上述代码中: * VARselect 函数用于选择滞后阶数。 * lag.max 参数指定要考虑的最大滞后阶数。 * type 参数指定模型中包含的外生变量类型,“const” 表示包含常数项。
根据确定的滞后阶数,使用 VAR 函数拟合 VAR 模型。
# 根据选择的滞后阶数拟合VAR模型
lag_order <- lag_selection$selection[1]
fit_var <- VAR(Canada, p = lag_order, type = "const")
print(fit_var)##
## VAR Estimation Results:
## =======================
##
## Estimated coefficients for equation e:
## ======================================
## Call:
## e = e.l1 + prod.l1 + rw.l1 + U.l1 + e.l2 + prod.l2 + rw.l2 + U.l2 + e.l3 + prod.l3 + rw.l3 + U.l3 + const
##
## e.l1 prod.l1 rw.l1 U.l1
## 1.75274 0.16962 -0.08260 0.09952
## e.l2 prod.l2 rw.l2 U.l2
## -1.18385 -0.10574 -0.02439 -0.05077
## e.l3 prod.l3 rw.l3 U.l3
## 0.58725 0.01054 0.03824 0.34139
## const
## -150.68737
##
##
## Estimated coefficients for equation prod:
## =========================================
## Call:
## prod = e.l1 + prod.l1 + rw.l1 + U.l1 + e.l2 + prod.l2 + rw.l2 + U.l2 + e.l3 + prod.l3 + rw.l3 + U.l3 + const
##
## e.l1 prod.l1 rw.l1 U.l1
## -0.14880 1.14799 0.02359 -0.65814
## e.l2 prod.l2 rw.l2 U.l2
## -0.18165 -0.19627 -0.20337 0.82237
## e.l3 prod.l3 rw.l3 U.l3
## 0.57495 0.04415 0.09337 0.40078
## const
## -195.86985
##
##
## Estimated coefficients for equation rw:
## =======================================
## Call:
## rw = e.l1 + prod.l1 + rw.l1 + U.l1 + e.l2 + prod.l2 + rw.l2 + U.l2 + e.l3 + prod.l3 + rw.l3 + U.l3 + const
##
## e.l1 prod.l1 rw.l1 U.l1
## -4.716e-01 -6.500e-02 9.091e-01 -7.941e-04
## e.l2 prod.l2 rw.l2 U.l2
## 6.667e-01 -2.164e-01 -1.457e-01 -3.014e-01
## e.l3 prod.l3 rw.l3 U.l3
## -1.289e-01 2.140e-01 1.902e-01 1.506e-01
## const
## -1.167e+01
##
##
## Estimated coefficients for equation U:
## ======================================
## Call:
## U = e.l1 + prod.l1 + rw.l1 + U.l1 + e.l2 + prod.l2 + rw.l2 + U.l2 + e.l3 + prod.l3 + rw.l3 + U.l3 + const
##
## e.l1 prod.l1 rw.l1 U.l1 e.l2
## -0.61773 -0.09778 0.01455 0.65976 0.51811
## prod.l2 rw.l2 U.l2 e.l3 prod.l3
## 0.08799 0.06993 -0.08099 -0.03006 -0.01092
## rw.l3 U.l3 const
## -0.03909 0.06684 114.36732在上述代码中:p 参数设置为通过信息准则选择的滞后阶数。
拟合 VAR 模型后,需要对模型进行诊断,检查模型是否合适。常见的诊断方法包括:
- 残差的自相关检验
##
## Portmanteau Test (asymptotic)
##
## data: Residuals of VAR object fit_var
## Chi-squared = 92, df = 112, p-value = 0.9- 残差的正态性检验
## $JB
##
## JB-Test (multivariate)
##
## data: Residuals of VAR object fit_var
## Chi-squared = 16, df = 8, p-value = 0.04
##
##
## $Skewness
##
## Skewness only (multivariate)
##
## data: Residuals of VAR object fit_var
## Chi-squared = 6.5, df = 4, p-value = 0.2
##
##
## $Kurtosis
##
## Kurtosis only (multivariate)
##
## data: Residuals of VAR object fit_var
## Chi-squared = 9.7, df = 4, p-value = 0.05- 格兰杰因果关系检验
可以检验每个变量对其他变量是否存在格兰杰因果关系。
## Warning in causality(fit_var):
## Argument 'cause' has not been specified;
## using first variable in 'x$y' (e) as cause variable.## $Granger
##
## Granger causality H0: e do not Granger-cause
## prod rw U
##
## data: VAR object fit_var
## F-Test = 3.9, df1 = 9, df2 = 272, p-value =
## 1e-04
##
##
## $Instant
##
## H0: No instantaneous causality between: e
## and prod rw U
##
## data: VAR object fit_var
## Chi-squared = 29, df = 3, p-value = 3e-06使用拟合好的 VAR 模型进行预测。
## $e
## fcst lower upper CI
## [1,] 962.8 962.2 963.5 0.6661
## [2,] 964.1 962.8 965.5 1.3191
## [3,] 965.5 963.7 967.4 1.8559
##
## $prod
## fcst lower upper CI
## [1,] 417.4 416.2 418.7 1.277
## [2,] 418.1 416.1 420.1 1.958
## [3,] 418.8 416.4 421.3 2.457
##
## $rw
## fcst lower upper CI
## [1,] 470.0 468.6 471.5 1.490
## [2,] 470.8 468.8 472.9 2.061
## [3,] 471.3 468.9 473.7 2.378
##
## $U
## fcst lower upper CI
## [1,] 6.484 5.932 7.037 0.5524
## [2,] 5.831 4.922 6.740 0.9090
## [3,] 5.167 3.919 6.415 1.2480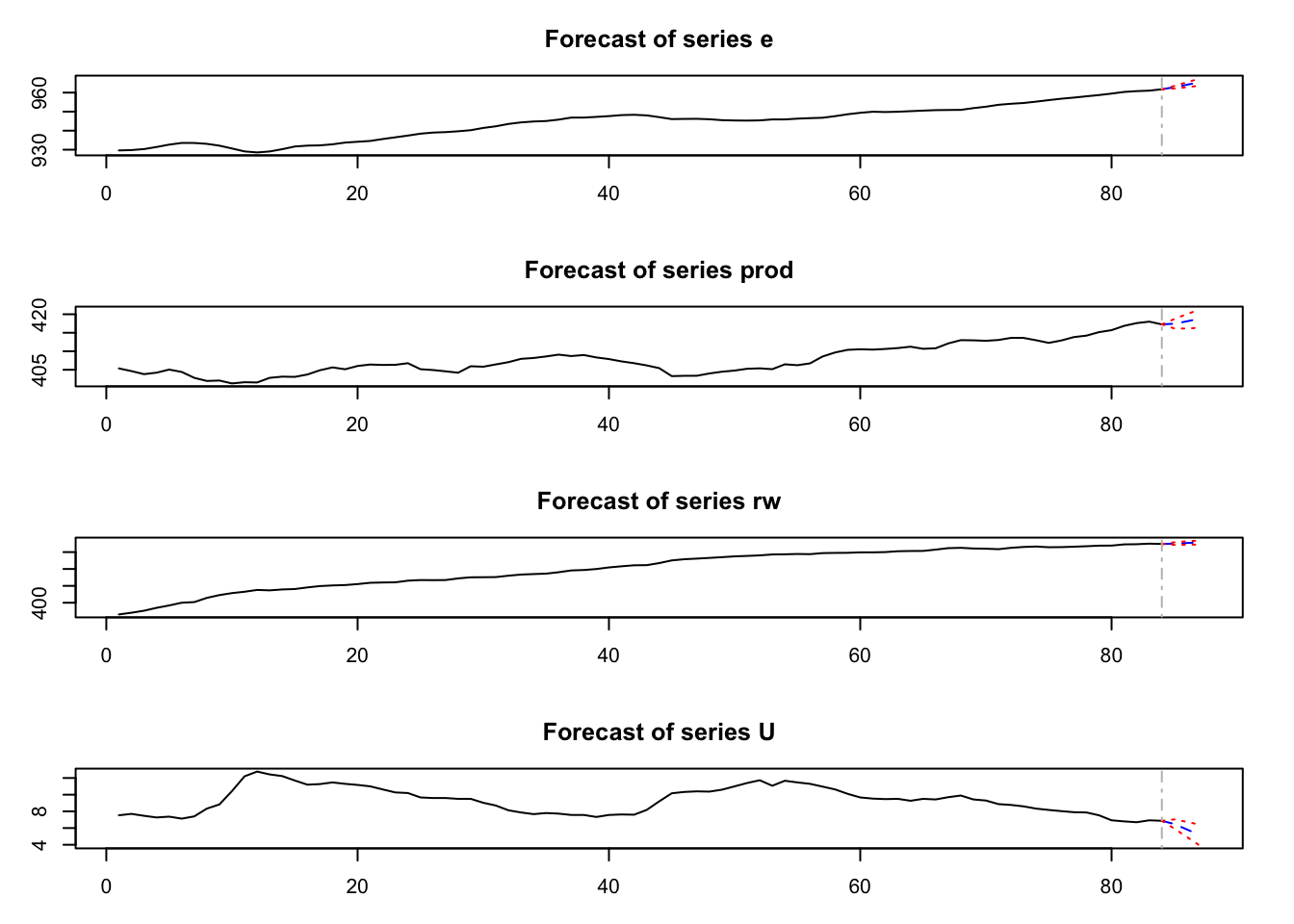
在上述代码中: * n.ahead 参数指定预测的期数。 * plot 函数用于绘制预测结果,展示预测值和置信区间。