第 5 章 时间序列分析中的 GARCH 模型
5.1 如何拟合 ARCH 模型?
在 R 语言中拟合自回归条件异方差(ARCH)模型,常用的包是 fGarch。
首先加载 fGarch 包,如果没有安装,需先安装再加载。
## NOTE: Packages 'fBasics', 'timeDate', and 'timeSeries' are no longer
## attached to the search() path when 'fGarch' is attached.
##
## If needed attach them yourself in your R script by e.g.,
## require("timeSeries")假设已有金融时间序列数据,将其转换为合适的格式。这里以简单收益率序列为例,通常需要对价格序列进行对数差分来计算收益率。
# 示例价格序列
price <- c(100, 102, 105, 103, 107, 104, 109, 106, 110, 108)
# 计算对数收益率
returns <- diff(log(price))
# 将收益率转换为时间序列对象
ts_returns <- ts(returns, frequency = 1)使用 garchFit 函数来拟合 ARCH 模型。ARCH (p) 模型中,p 表示 ARCH 项的阶数。
##
## Series Initialization:
## ARMA Model: arma
## Formula Mean: ~ arma(0, 0)
## GARCH Model: garch
## Formula Variance: ~ garch(1, 0)
## ARMA Order: 0 0
## Max ARMA Order: 0
## GARCH Order: 1 0
## Max GARCH Order: 1
## Maximum Order: 1
## Conditional Dist: norm
## h.start: 2
## llh.start: 1
## Length of Series: 9
## Recursion Init: mci
## Series Scale: 0.03142
##
## Parameter Initialization:
## Initial Parameters: $params
## Limits of Transformations: $U, $V
## Which Parameters are Fixed? $includes
## Parameter Matrix:
## U V params includes
## mu -2.722e+00 2.722 0.2722 TRUE
## omega 1.000e-06 100.000 0.1000 TRUE
## alpha1 1.000e-08 1.000 0.1000 TRUE
## gamma1 -1.000e+00 1.000 0.1000 FALSE
## delta 0.000e+00 2.000 2.0000 FALSE
## skew 1.000e-01 10.000 1.0000 FALSE
## shape 1.000e+00 10.000 4.0000 FALSE
## Index List of Parameters to be Optimized:
## mu omega alpha1
## 1 2 3
## Persistence: 0.1
##
##
## --- START OF TRACE ---
## Selected Algorithm: nlminb
##
## R coded nlminb Solver:
##
## 0: 21.402773: 0.272170 0.100000 0.100000
## 1: 12.665457: 0.269698 0.869289 0.738836
## 2: 12.635209: 0.281595 0.815430 0.781563
## 3: 12.332695: 0.301814 0.399306 1.00000
## 4: 12.164310: 0.296407 0.283343 0.900445
## 5: 12.145624: 0.268870 0.218458 0.616603
## 6: 12.060826: 0.260141 0.465170 0.434621
## 7: 12.053330: 0.261397 0.425275 0.530211
## 8: 12.050975: 0.262984 0.402514 0.543349
## 9: 12.050357: 0.263041 0.380110 0.557084
## 10: 12.050344: 0.263112 0.383421 0.554449
## 11: 12.050343: 0.263101 0.383242 0.554569
## 12: 12.050343: 0.263102 0.383240 0.554568
##
## Final Estimate of the Negative LLH:
## LLH: -19.09 norm LLH: -2.121
## mu omega alpha1
## 0.0082663 0.0003783 0.5545684
##
## R-optimhess Difference Approximated Hessian Matrix:
## mu omega alpha1
## mu -33343.90 51404 25.133
## omega 51403.78 -7745216 -4820.550
## alpha1 25.13 -4821 -4.451
## attr(,"time")
## Time difference of 0.002612 secs
##
## --- END OF TRACE ---
##
##
## Time to Estimate Parameters:
## Time difference of 0.01715 secs##
## Title:
## GARCH Modelling
##
## Call:
## garchFit(formula = ~garch(1, 0), data = ts_returns)
##
## Mean and Variance Equation:
## data ~ garch(1, 0)
## <environment: 0x7febd9542df0>
## [data = ts_returns]
##
## Conditional Distribution:
## norm
##
## Coefficient(s):
## mu omega alpha1
## 0.00826632 0.00037831 0.55456841
##
## Std. Errors:
## based on Hessian
##
## Error Analysis:
## Estimate Std. Error t value Pr(>|t|)
## mu 0.0082663 0.0055073 1.501 0.133
## omega 0.0003783 0.0006316 0.599 0.549
## alpha1 0.5545684 0.8306641 0.668 0.504
##
## Log Likelihood:
## 19.09 normalized: 2.121
##
## Description:
## Fri Jul 11 18:40:06 2025 by user:在上述代码中:formula = ~garch(1,0) 表示拟合 ARCH (1) 模型,garch(p,q) 中 p 是 ARCH 项的阶数,q 是 GARCH 项的阶数(这里为 0,因为是纯粹的 ARCH 模型)。
data = ts_returns 指定用于拟合模型的时间序列数据为收益率序列。
拟合模型后,需要对模型进行诊断,以检查模型是否合适。常见的诊断方法包括检查残差的自相关和条件异方差性。
检查残差自相关
# 提取标准化残差
std_residuals <- residuals(fit_arch, standardize = TRUE)
# 绘制标准化残差的自相关函数图
acf(std_residuals, main = "ACF of Standardized Residuals")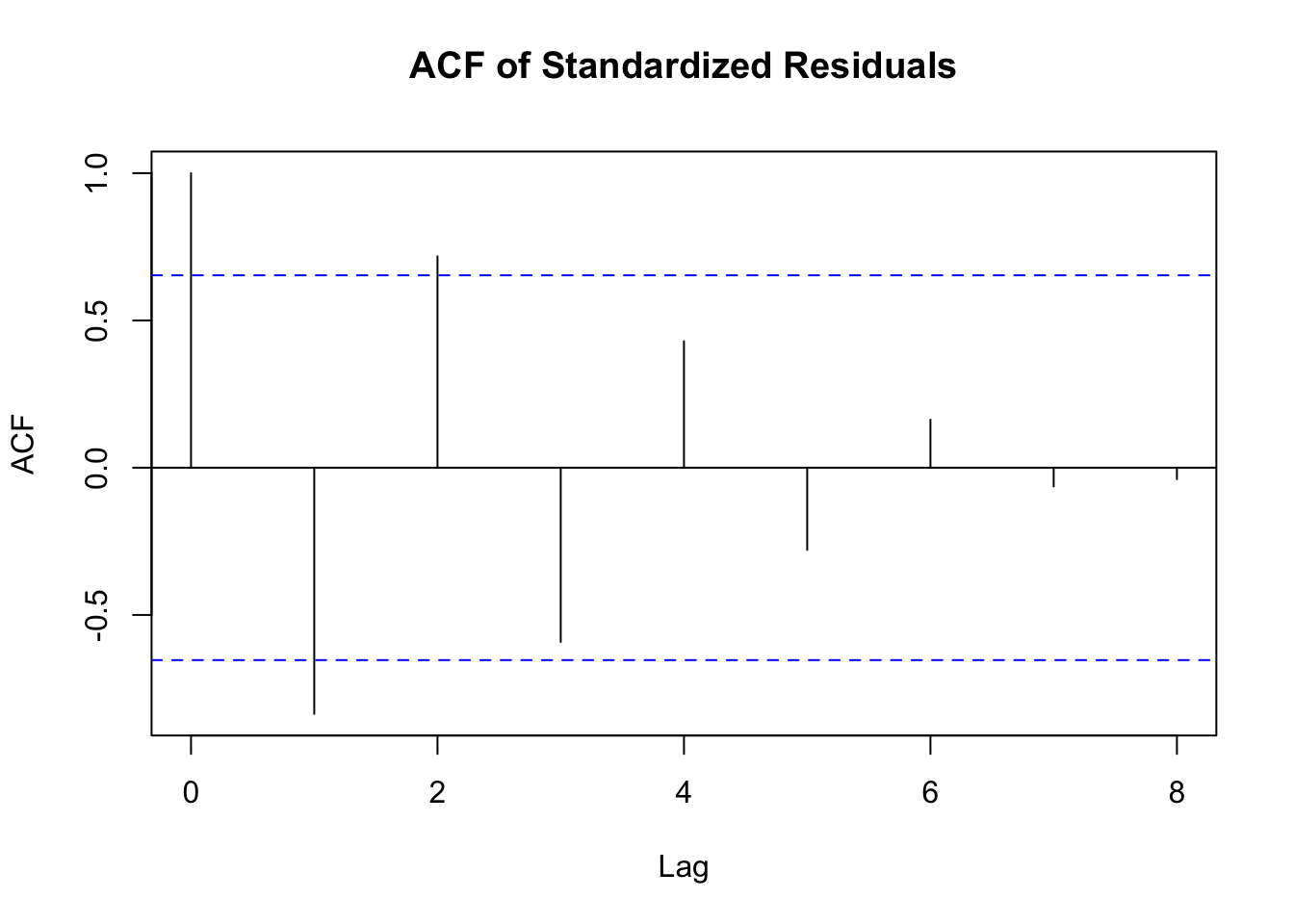
检查条件异方差性
##
## Attaching package: 'FinTS'## The following object is masked from 'package:forecast':
##
## Acf# 进行ARCH - LM检验
if(!inherits(std_residuals, "ts")) {
std_residuals <- ts(std_residuals, frequency = 1)
}
arch_lm_test <- ArchTest(std_residuals,lags = 2)
print(arch_lm_test)##
## ARCH LM-test; Null hypothesis: no ARCH
## effects
##
## data: std_residuals
## Chi-squared = 2.1, df = 2, p-value = 0.3使用拟合好的 ARCH 模型进行预测。
## meanForecast meanError standardDeviation
## 1 0.008266 0.02777 0.02777
## 2 0.008266 0.02839 0.02839
## 3 0.008266 0.02873 0.028735.2 如何拟合 GARCH 模型?
在 R 语言中拟合广义自回归条件异方差(GARCH)模型,通常使用fGarch包。
如果尚未安装fGarch包,需要先进行安装,然后加载它。
假设我们有一个金融时间序列数据,例如股票价格序列。通常需要先将价格序列转换为收益率序列,一般采用对数收益率。
# 示例价格序列
price <- c(100, 102, 105, 103, 107, 104, 109, 106, 110, 108)
# 计算对数收益率
returns <- diff(log(price))
# 将收益率转换为时间序列对象
ts_returns <- ts(returns, frequency = 1)使用garchFit函数来拟合 GARCH (p,q) 模型,其中p是 ARCH 项的阶数,q是 GARCH 项的阶数。
##
## Series Initialization:
## ARMA Model: arma
## Formula Mean: ~ arma(0, 0)
## GARCH Model: garch
## Formula Variance: ~ garch(1, 1)
## ARMA Order: 0 0
## Max ARMA Order: 0
## GARCH Order: 1 1
## Max GARCH Order: 1
## Maximum Order: 1
## Conditional Dist: norm
## h.start: 2
## llh.start: 1
## Length of Series: 9
## Recursion Init: mci
## Series Scale: 0.03142
##
## Parameter Initialization:
## Initial Parameters: $params
## Limits of Transformations: $U, $V
## Which Parameters are Fixed? $includes
## Parameter Matrix:
## U V params includes
## mu -2.722e+00 2.722 0.2722 TRUE
## omega 1.000e-06 100.000 0.1000 TRUE
## alpha1 1.000e-08 1.000 0.1000 TRUE
## gamma1 -1.000e+00 1.000 0.1000 FALSE
## beta1 1.000e-08 1.000 0.8000 TRUE
## delta 0.000e+00 2.000 2.0000 FALSE
## skew 1.000e-01 10.000 1.0000 FALSE
## shape 1.000e+00 10.000 4.0000 FALSE
## Index List of Parameters to be Optimized:
## mu omega alpha1 beta1
## 1 2 3 5
## Persistence: 0.9
##
##
## --- START OF TRACE ---
## Selected Algorithm: nlminb
##
## R coded nlminb Solver:
##
## 0: 12.230474: 0.272170 0.100000 0.100000 0.800000
## 1: 12.221270: 0.272164 0.114664 0.110886 0.811272
## 2: 12.215804: 0.272932 0.126638 0.100453 0.797114
## 3: 12.213032: 0.274780 0.158682 0.0823255 0.776116
## 4: 12.208664: 0.277941 0.210107 0.0901593 0.708816
## 5: 12.146469: 0.305662 0.710939 0.223365 1.00000e-08
## 6: 12.135791: 0.293042 0.700899 0.230291 1.00000e-08
## 7: 12.093912: 0.243210 0.580573 0.330530 1.00000e-08
## 8: 12.071014: 0.242315 0.486770 0.415371 1.00000e-08
## 9: 12.063518: 0.272571 0.324203 0.570067 1.00000e-08
## 10: 12.054351: 0.262584 0.419094 0.484321 1.00000e-08
## 11: 12.053175: 0.262740 0.398924 0.505071 1.00000e-08
## 12: 12.052426: 0.263777 0.384312 0.523673 1.00000e-08
## 13: 12.051633: 0.263935 0.376281 0.539180 1.00000e-08
## 14: 12.050588: 0.263813 0.374040 0.557101 1.00000e-08
## 15: 12.050363: 0.263297 0.379452 0.558062 1.00000e-08
## 16: 12.050344: 0.263145 0.382569 0.555553 1.00000e-08
## 17: 12.050343: 0.263099 0.383202 0.554672 1.00000e-08
## 18: 12.050343: 0.263103 0.383244 0.554569 1.00000e-08
## 19: 12.050343: 0.263102 0.383240 0.554568 1.00000e-08
##
## Final Estimate of the Negative LLH:
## LLH: -19.09 norm LLH: -2.121
## mu omega alpha1 beta1
## 8.266e-03 3.783e-04 5.546e-01 1.000e-08
##
## R-optimhess Difference Approximated Hessian Matrix:
## mu omega alpha1 beta1
## mu -33343.89 51403 25.133 24.856
## omega 51402.79 -7745215 -4820.553 -5378.501
## alpha1 25.13 -4821 -4.451 -3.783
## beta1 24.86 -5379 -3.783 -4.339
## attr(,"time")
## Time difference of 0.004818 secs
##
## --- END OF TRACE ---
##
##
## Time to Estimate Parameters:
## Time difference of 0.02455 secs##
## Title:
## GARCH Modelling
##
## Call:
## garchFit(formula = ~garch(1, 1), data = ts_returns)
##
## Mean and Variance Equation:
## data ~ garch(1, 1)
## <environment: 0x7febdbc819d8>
## [data = ts_returns]
##
## Conditional Distribution:
## norm
##
## Coefficient(s):
## mu omega alpha1 beta1
## 0.00826631 0.00037831 0.55456807 0.00000001
##
## Std. Errors:
## based on Hessian
##
## Error Analysis:
## Estimate Std. Error t value Pr(>|t|)
## mu 8.266e-03 5.521e-03 1.497 0.134
## omega 3.783e-04 9.752e-04 0.388 0.698
## alpha1 5.546e-01 9.377e-01 0.591 0.554
## beta1 1.000e-08 1.456e+00 0.000 1.000
##
## Log Likelihood:
## 19.09 normalized: 2.121
##
## Description:
## Fri Jul 11 18:40:06 2025 by user:在上述代码中: formula = ~garch(1,1)指定了要拟合的是 GARCH (1,1) 模型。garch(p,q)中的p和q分别对应 ARCH 项和 GARCH 项的阶数。 data = ts_returns表示使用之前计算得到的收益率时间序列数据进行模型拟合。
拟合模型后,需要对模型进行诊断以检查其合理性。常见的诊断方法包括:
检查残差的自相关
# 提取标准化残差
std_residuals <- residuals(fit_garch, standardize = TRUE)
# 绘制标准化残差的自相关函数图
acf(std_residuals, main = "ACF of Standardized Residuals")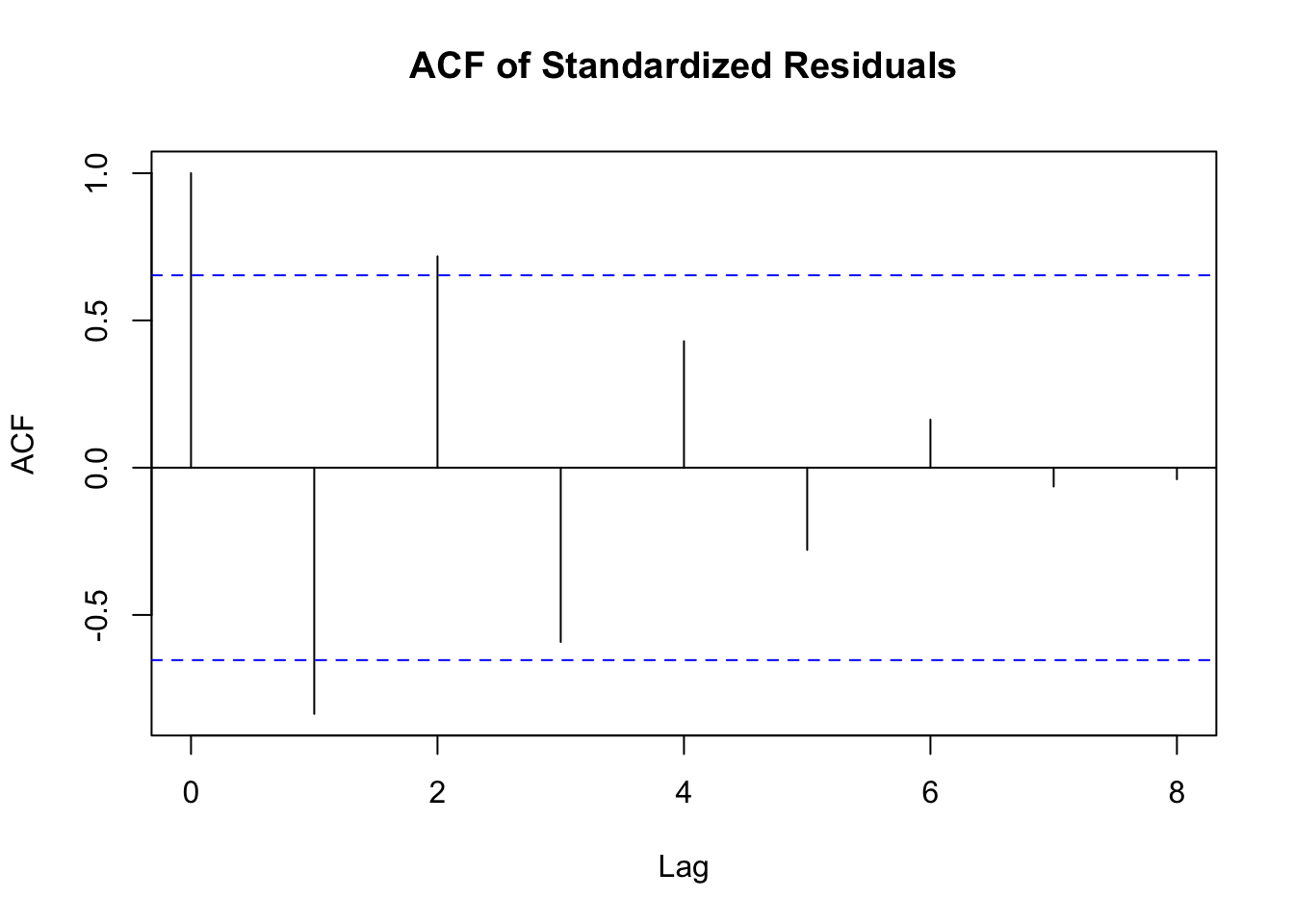
检查条件异方差性
##
## ARCH LM-test; Null hypothesis: no ARCH
## effects
##
## data: std_residuals
## Chi-squared = 2.1, df = 2, p-value = 0.3使用拟合好的 GARCH 模型进行预测。
## meanForecast meanError standardDeviation
## 1 0.008266 0.02777 0.02777
## 2 0.008266 0.02839 0.02839
## 3 0.008266 0.02873 0.028735.3 如何拟合 mgarch 模型?
在 R 语言中,若要拟合多元广义自回归条件异方差(MGARCH)模型,可借助rmgarch包来完成。在此过程中,可能还需加载fGarch包,因为rmgarch包的某些功能依赖于它。若尚未安装这两个包,需先进行安装。
具体操作如下:
# 安装 rmgarch 包(如果未安装)
# install.packages("rmgarch")
# 安装 fGarch 包(如果未安装)
# install.packages("fGarch")
library(fBasics)
library(rmgarch)## Loading required package: rugarch## Loading required package: parallel##
## Attaching package: 'rugarch'## The following objects are masked from 'package:fBasics':
##
## qgh, qnig##
## Attaching package: 'rmgarch'## The following objects are masked from 'package:xts':
##
## first, last假设手头拥有多个相关的金融时间序列数据,比如多个股票的收益率序列。首先要将这些序列整理为合适的格式,一般是构建成一个矩阵或数据框,其中每一列代表一个时间序列。以下代码展示了如何从雅虎财经获取数据,并将其处理为所需格式,同时计算对数收益率并去除缺失值:
## Loading required package: TTR##
## Attaching package: 'TTR'## The following object is masked from 'package:fBasics':
##
## volatility## The following object is masked from 'package:fGarch':
##
## volatility#load data, time series closing prices, 10 year sample
#DAX 30
getSymbols('^GDAXI', src='yahoo', from="2025-01-01", to="2055-05-31")## [1] "GDAXI"GDAXI.DE=GDAXI[ , "GDAXI.Close"]
#S&P 500
getSymbols('^GSPC', src='yahoo', from="2025-01-01", to="2055-05-31")## [1] "GSPC"GSPC=GSPC[ , "GSPC.Close"]
#Credit Suisse Commodity Return Strat I
getSymbols('CRSOX', src='yahoo', from="2025-01-01", to="2055-05-31")## [1] "CRSOX"CRSOX=CRSOX[ , "CRSOX.Close"]
#iShares MSCI Emerging Markets
getSymbols('EEM', src='yahoo', from="2025-01-01", to="2055-05-31")## [1] "EEM"EEM=EEM[ , "EEM.Close"]
merged_data <- merge(GDAXI.DE, GSPC, CRSOX, EEM)
# 转换回 data.frame
Dat <- as.data.frame(merged_data)
Dat<-apply(Dat,2,function(x) Delt(x,k=1,type="log"))
Dat <- na.omit(Dat)rmgarch包提供了多种 MGARCH 模型形式,其中常见的有 BEKK、CCC 等。这里以 BEKK (1,1) 模型为例来展示模型的构建。
xspec <- ugarchspec(mean.model = list(armaOrder = c(1, 1)),
variance.model = list(garchOrder = c(1,1), model ='sGARCH'),
distribution.model = 'norm')
uspec = multispec(replicate(4, xspec))
spec1 = dccspec(uspec = uspec, dccOrder = c(1, 1), distribution ='mvnorm')
spec1a = dccspec(uspec = uspec, dccOrder = c(1, 1), model='aDCC', distribution ='mvnorm')在上述代码片段中: * ugarchspec用于定义单变量 GARCH 模型部分。其中,variance.model里的model = “sGARCH”表明采用标准 GARCH 模型,garchOrder = c(1, 1)将 GARCH 项和 ARCH 项的阶数都设定为 1。mean.model中的armaOrder = c(1, 1)意味着均值模型包含一阶自回归和一阶移动平均项 。 * uspec通过multispec函数和replicate函数,将单变量 GARCH 模型规范xspec复制 4 份,以适配多元模型。 * spec1使用dccspec定义了一个普通的动态条件相关(DCC)模型,dccOrder = c(1, 1)指定 DCC 模型的阶数,distribution =’mvnorm’表示假设数据服从多元正态分布。 * spec1a同样使用dccspec,不过定义的是一个非对称动态条件相关(aDCC)模型,其他设置与spec1相同。 完成模型规范定义后,即可使用这些规范和处理好的数据进行模型拟合,代码如下:
cl = makePSOCKcluster(2)
multf = multifit(uspec, Dat, cluster = cl)
fit1 = dccfit(spec1, data = Dat, fit.control = list(eval.se = TRUE), fit = multf, cluster = cl)
fit_adcc = dccfit(spec1a, data = Dat, fit.control = list(eval.se = TRUE), fit = multf, cluster = cl)
stopCluster(cl)
print(fit1) ##
## *---------------------------------*
## * DCC GARCH Fit *
## *---------------------------------*
##
## Distribution : mvnorm
## Model : DCC(1,1)
## No. Parameters : 32
## [VAR GARCH DCC UncQ] : [0+24+2+6]
## No. Series : 4
## No. Obs. : 118
## Log-Likelihood : 1534
## Av.Log-Likelihood : 13
##
## Optimal Parameters
## -----------------------------------
## Estimate Std. Error
## [GDAXI.Close].mu 0.002194 0.001137
## [GDAXI.Close].ar1 0.197088 0.354794
## [GDAXI.Close].ma1 -0.068340 0.377016
## [GDAXI.Close].omega 0.000020 0.000012
## [GDAXI.Close].alpha1 0.360916 0.130517
## [GDAXI.Close].beta1 0.524267 0.152705
## [GSPC.Close].mu 0.000992 0.000903
## [GSPC.Close].ar1 -0.491311 0.500944
## [GSPC.Close].ma1 0.362061 0.716581
## [GSPC.Close].omega 0.000006 0.000108
## [GSPC.Close].alpha1 0.208162 0.334588
## [GSPC.Close].beta1 0.788124 0.446933
## [CRSOX.Close].mu 0.000206 0.000880
## [CRSOX.Close].ar1 0.292972 0.189983
## [CRSOX.Close].ma1 -0.149833 0.175832
## [CRSOX.Close].omega 0.000000 0.000001
## [CRSOX.Close].alpha1 0.000000 0.005107
## [CRSOX.Close].beta1 0.999000 0.004858
## [EEM.Close].mu 0.001754 0.000625
## [EEM.Close].ar1 0.732610 0.129026
## [EEM.Close].ma1 -0.903833 0.040540
## [EEM.Close].omega 0.000028 0.000015
## [EEM.Close].alpha1 0.356457 0.211869
## [EEM.Close].beta1 0.472421 0.099939
## [Joint]dcca1 0.053915 0.035782
## [Joint]dccb1 0.237058 0.183194
## t value Pr(>|t|)
## [GDAXI.Close].mu 1.929910 0.053618
## [GDAXI.Close].ar1 0.555500 0.578553
## [GDAXI.Close].ma1 -0.181267 0.856158
## [GDAXI.Close].omega 1.636180 0.101802
## [GDAXI.Close].alpha1 2.765277 0.005687
## [GDAXI.Close].beta1 3.433208 0.000596
## [GSPC.Close].mu 1.098412 0.272025
## [GSPC.Close].ar1 -0.980771 0.326706
## [GSPC.Close].ma1 0.505262 0.613375
## [GSPC.Close].omega 0.051674 0.958789
## [GSPC.Close].alpha1 0.622144 0.533847
## [GSPC.Close].beta1 1.763407 0.077832
## [CRSOX.Close].mu 0.234004 0.814982
## [CRSOX.Close].ar1 1.542099 0.123050
## [CRSOX.Close].ma1 -0.852139 0.394137
## [CRSOX.Close].omega 0.409955 0.681839
## [CRSOX.Close].alpha1 0.000000 1.000000
## [CRSOX.Close].beta1 205.630830 0.000000
## [EEM.Close].mu 2.805649 0.005022
## [EEM.Close].ar1 5.678017 0.000000
## [EEM.Close].ma1 -22.295000 0.000000
## [EEM.Close].omega 1.830470 0.067180
## [EEM.Close].alpha1 1.682440 0.092484
## [EEM.Close].beta1 4.727114 0.000002
## [Joint]dcca1 1.506778 0.131868
## [Joint]dccb1 1.294026 0.195656
##
## Information Criteria
## ---------------------
##
## Akaike -25.451
## Bayes -24.699
## Shibata -25.560
## Hannan-Quinn -25.146
##
##
## Elapsed time : 3.391##
## *---------------------------------*
## * DCC GARCH Fit *
## *---------------------------------*
##
## Distribution : mvnorm
## Model : aDCC(1,1)
## No. Parameters : 33
## [VAR GARCH DCC UncQ] : [0+24+3+6]
## No. Series : 4
## No. Obs. : 118
## Log-Likelihood : 1534
## Av.Log-Likelihood : 13
##
## Optimal Parameters
## -----------------------------------
## Estimate Std. Error
## [GDAXI.Close].mu 0.002194 0.001140
## [GDAXI.Close].ar1 0.197088 0.357555
## [GDAXI.Close].ma1 -0.068340 0.378972
## [GDAXI.Close].omega 0.000020 0.000012
## [GDAXI.Close].alpha1 0.360916 0.133331
## [GDAXI.Close].beta1 0.524267 0.153806
## [GSPC.Close].mu 0.000992 0.000908
## [GSPC.Close].ar1 -0.491311 0.503578
## [GSPC.Close].ma1 0.362061 0.730503
## [GSPC.Close].omega 0.000006 0.000111
## [GSPC.Close].alpha1 0.208162 0.343471
## [GSPC.Close].beta1 0.788124 0.456457
## [CRSOX.Close].mu 0.000206 0.000886
## [CRSOX.Close].ar1 0.292972 0.188904
## [CRSOX.Close].ma1 -0.149833 0.180547
## [CRSOX.Close].omega 0.000000 0.000001
## [CRSOX.Close].alpha1 0.000000 0.005096
## [CRSOX.Close].beta1 0.999000 0.004822
## [EEM.Close].mu 0.001754 0.000625
## [EEM.Close].ar1 0.732610 0.127187
## [EEM.Close].ma1 -0.903833 0.040502
## [EEM.Close].omega 0.000028 0.000015
## [EEM.Close].alpha1 0.356457 0.204838
## [EEM.Close].beta1 0.472421 0.099646
## [Joint]dcca1 0.053915 0.016528
## [Joint]dccb1 0.237059 0.025993
## [Joint]dccg1 0.000000 0.030432
## t value Pr(>|t|)
## [GDAXI.Close].mu 1.925130 0.054213
## [GDAXI.Close].ar1 0.551210 0.581490
## [GDAXI.Close].ma1 -0.180331 0.856893
## [GDAXI.Close].omega 1.631862 0.102708
## [GDAXI.Close].alpha1 2.706907 0.006791
## [GDAXI.Close].beta1 3.408627 0.000653
## [GSPC.Close].mu 1.092653 0.274546
## [GSPC.Close].ar1 -0.975641 0.329242
## [GSPC.Close].ma1 0.495632 0.620154
## [GSPC.Close].omega 0.050358 0.959837
## [GSPC.Close].alpha1 0.606054 0.544479
## [GSPC.Close].beta1 1.726612 0.084237
## [CRSOX.Close].mu 0.232610 0.816064
## [CRSOX.Close].ar1 1.550905 0.120925
## [CRSOX.Close].ma1 -0.829884 0.406605
## [CRSOX.Close].omega 0.410848 0.681184
## [CRSOX.Close].alpha1 0.000000 1.000000
## [CRSOX.Close].beta1 207.192869 0.000000
## [EEM.Close].mu 2.807533 0.004992
## [EEM.Close].ar1 5.760084 0.000000
## [EEM.Close].ma1 -22.315713 0.000000
## [EEM.Close].omega 1.835009 0.066504
## [EEM.Close].alpha1 1.740188 0.081826
## [EEM.Close].beta1 4.740982 0.000002
## [Joint]dcca1 3.262050 0.001106
## [Joint]dccb1 9.120050 0.000000
## [Joint]dccg1 0.000000 1.000000
##
## Information Criteria
## ---------------------
##
## Akaike -25.434
## Bayes -24.659
## Shibata -25.549
## Hannan-Quinn -25.119
##
##
## Elapsed time : 1.197模型拟合完成后,需要对模型进行诊断,以检查模型是否合适。诊断步骤如下:
# 提取 fit1 模型的标准化残差
std_residuals_fit1 <- residuals(fit1)
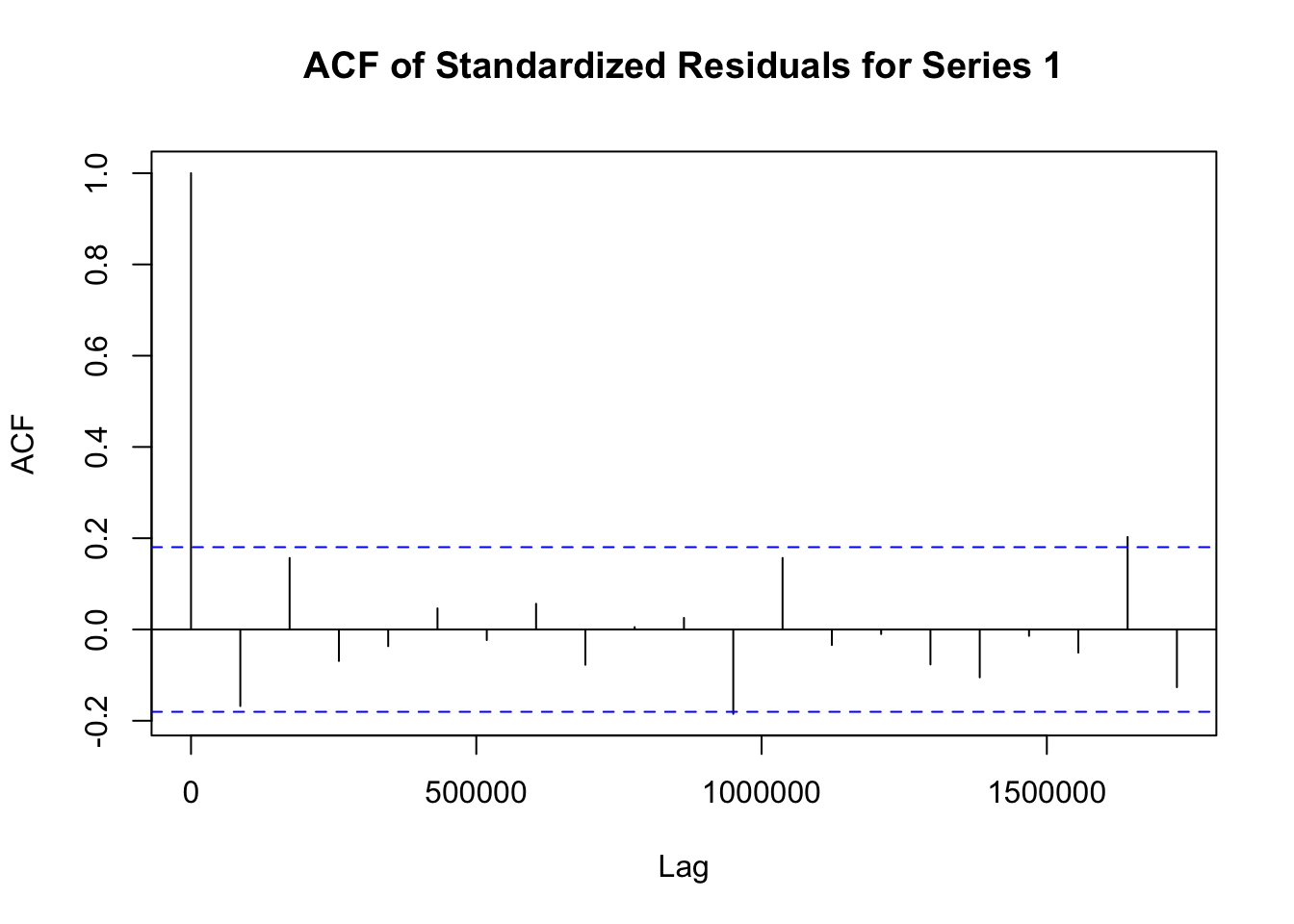
# 对 fit1 模型每个序列的标准化残差绘制自相关函数图
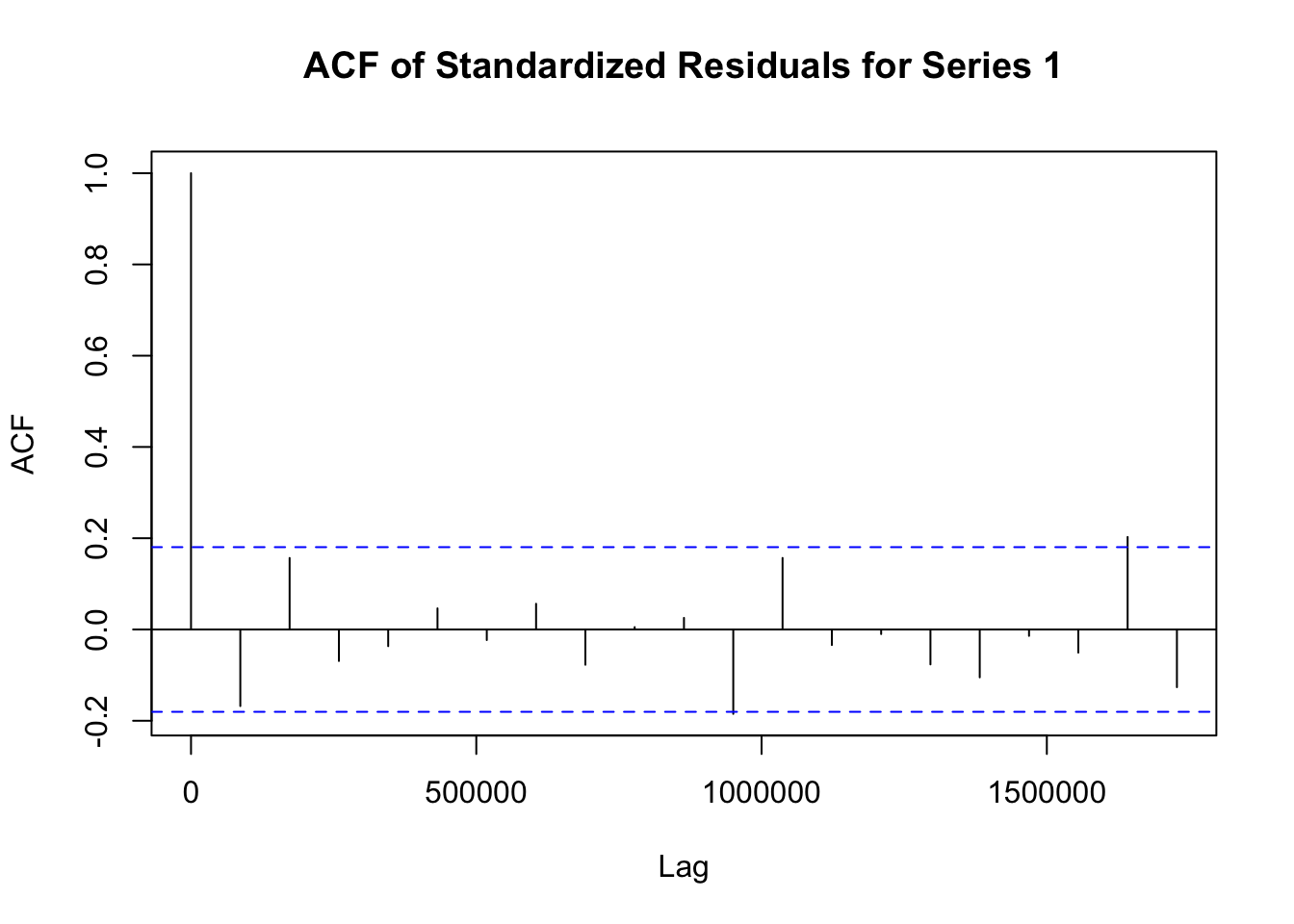
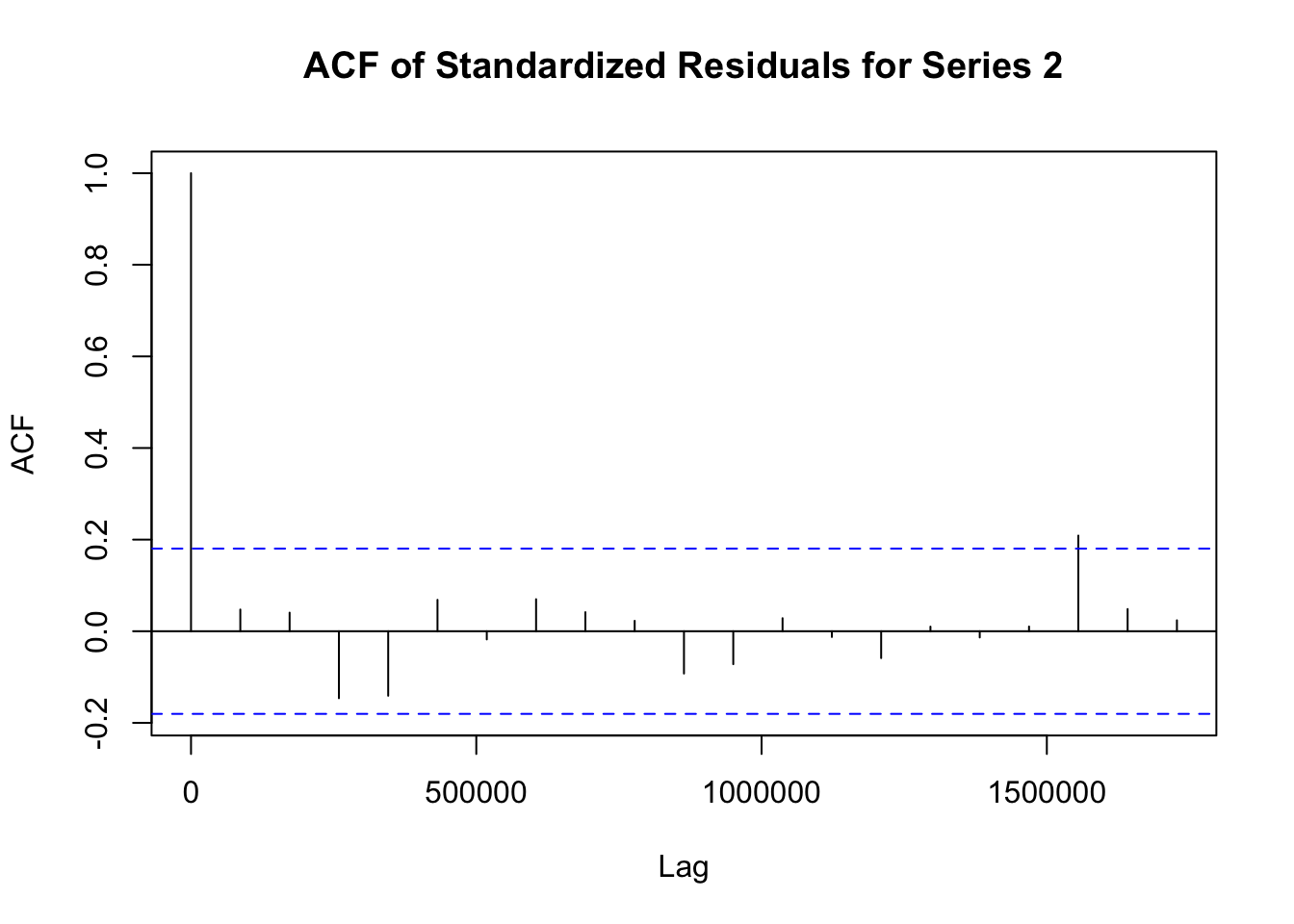
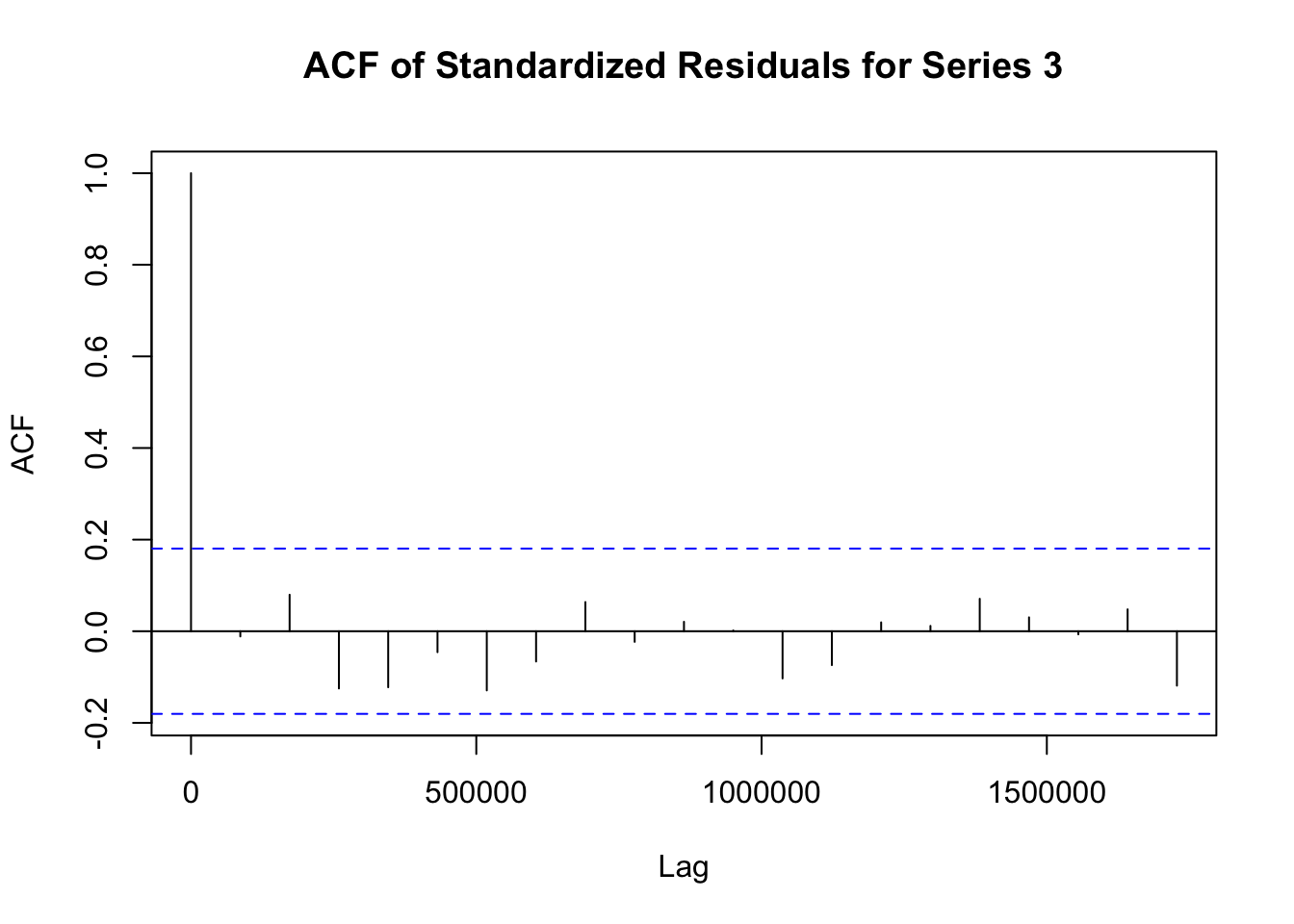
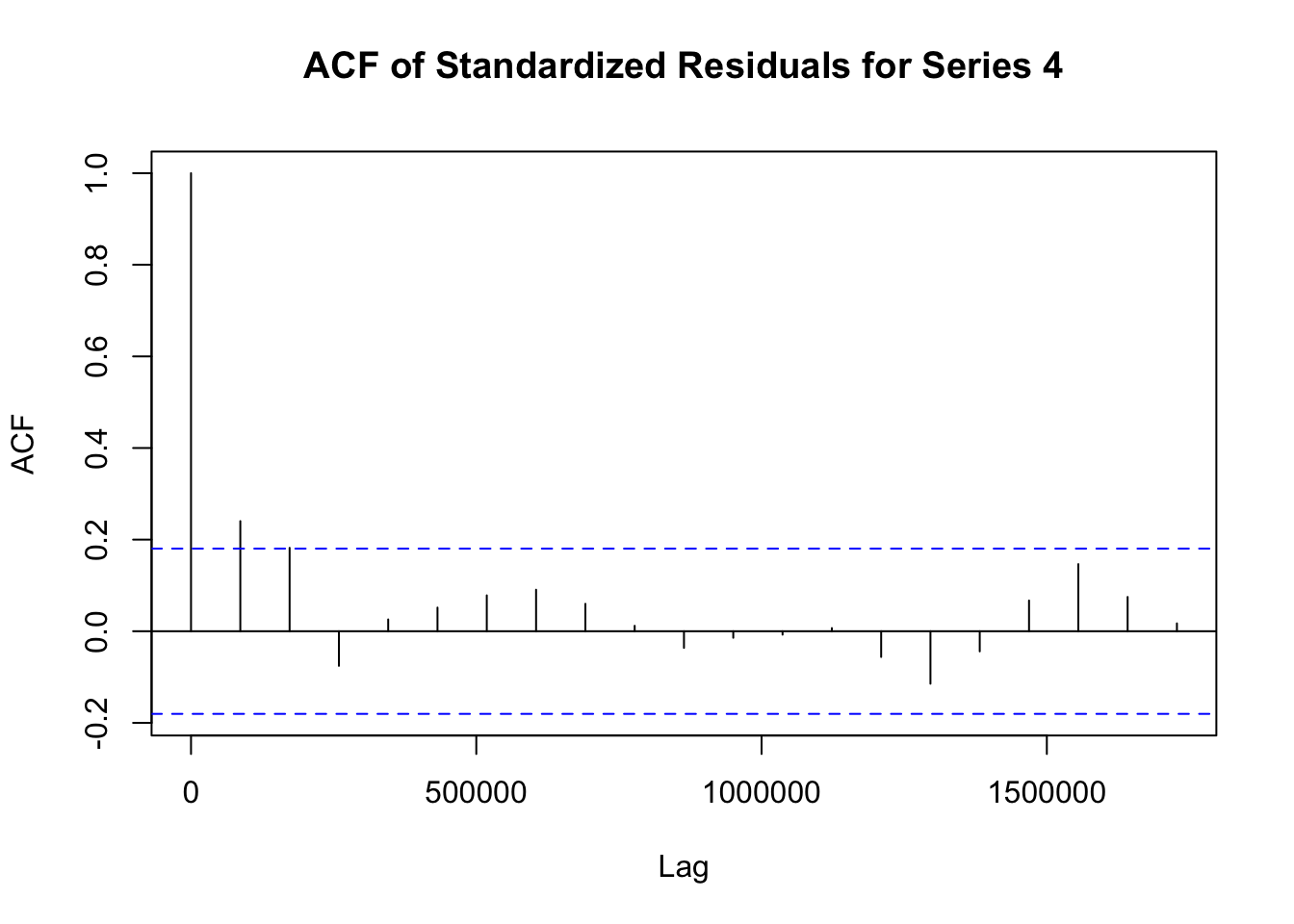
for (i in 1:ncol(std_residuals_fit1)) {
acf(std_residuals_fit1[, i], main = paste("ACF of Standardized Residuals for Series", i))
}
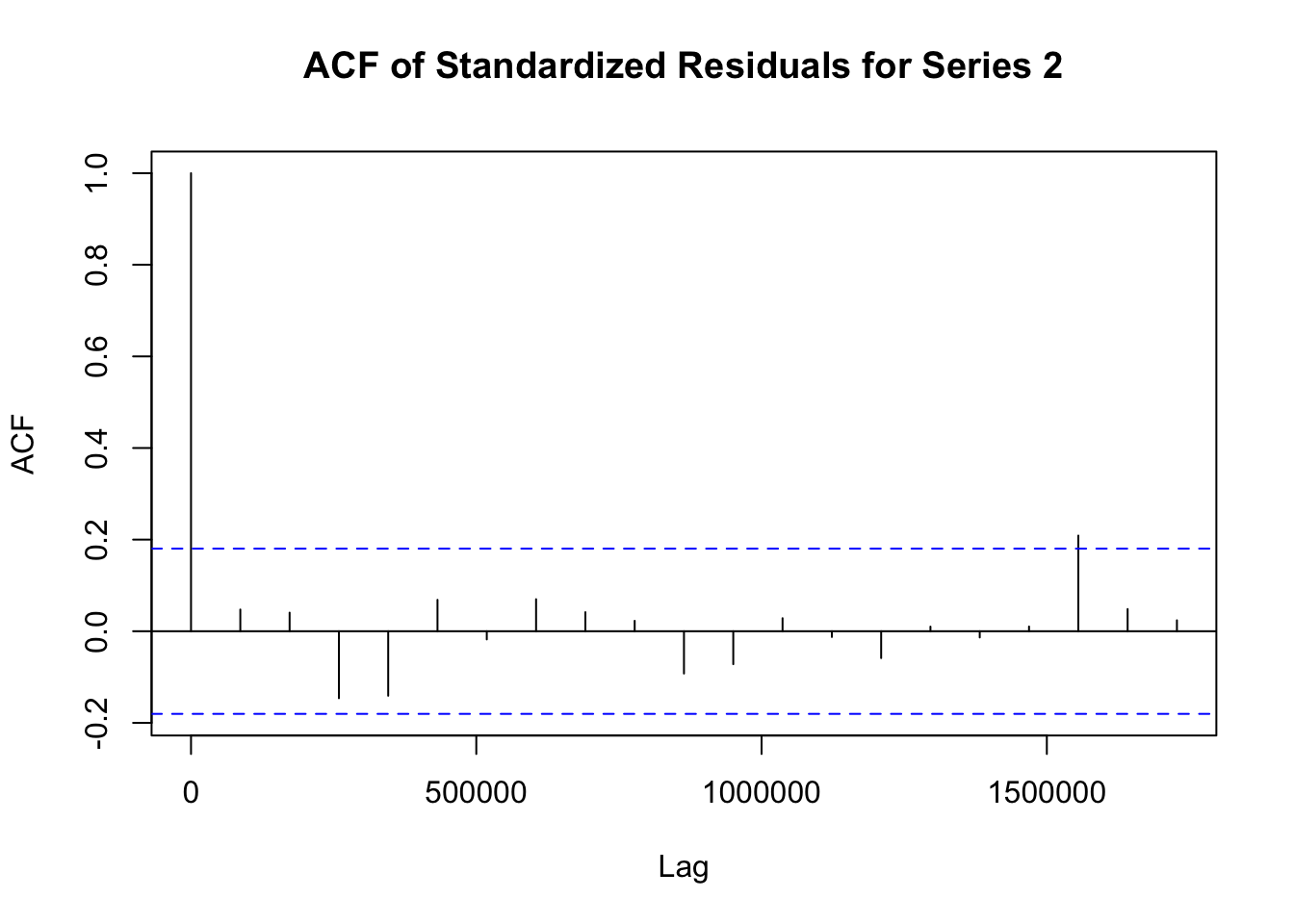
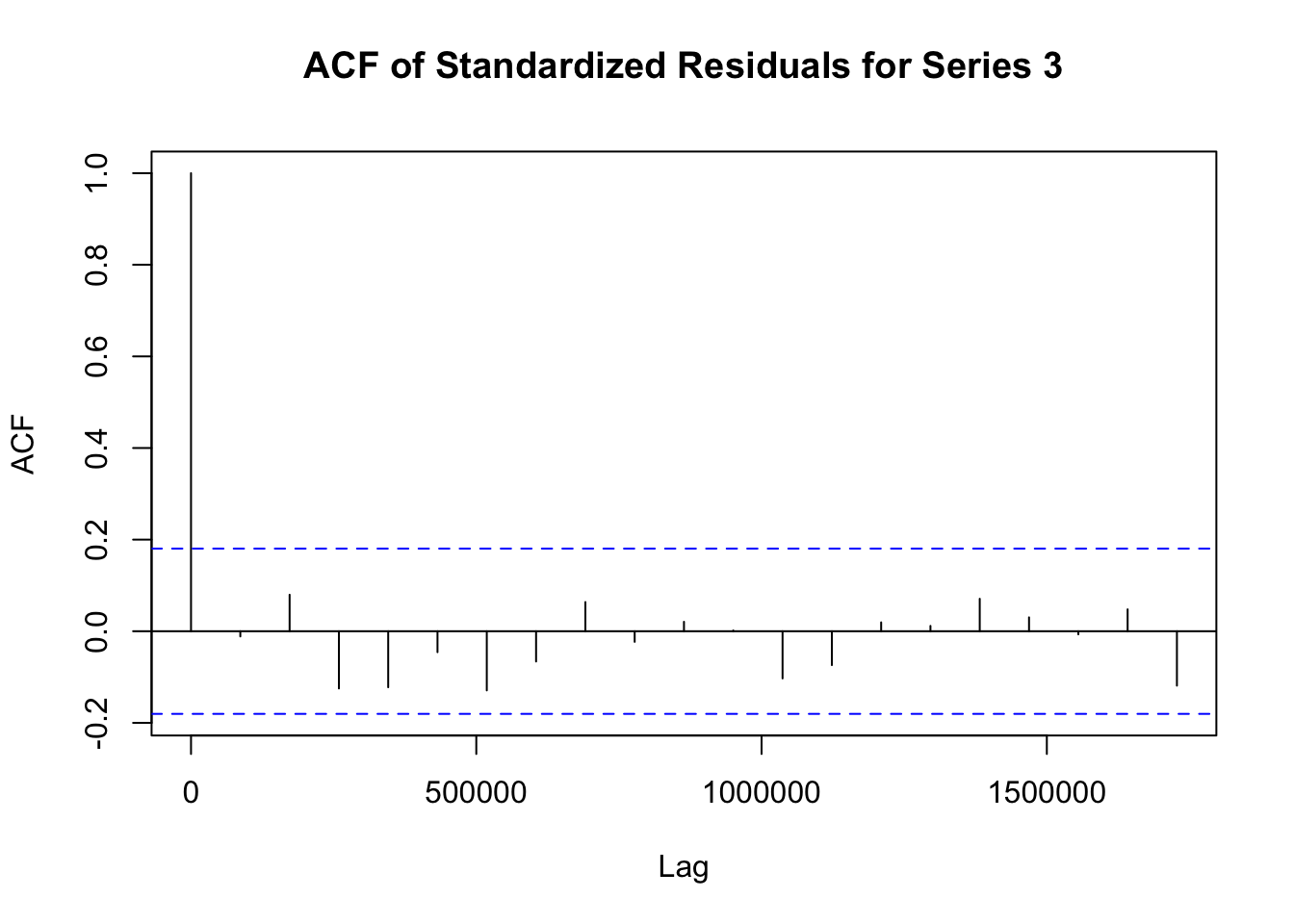
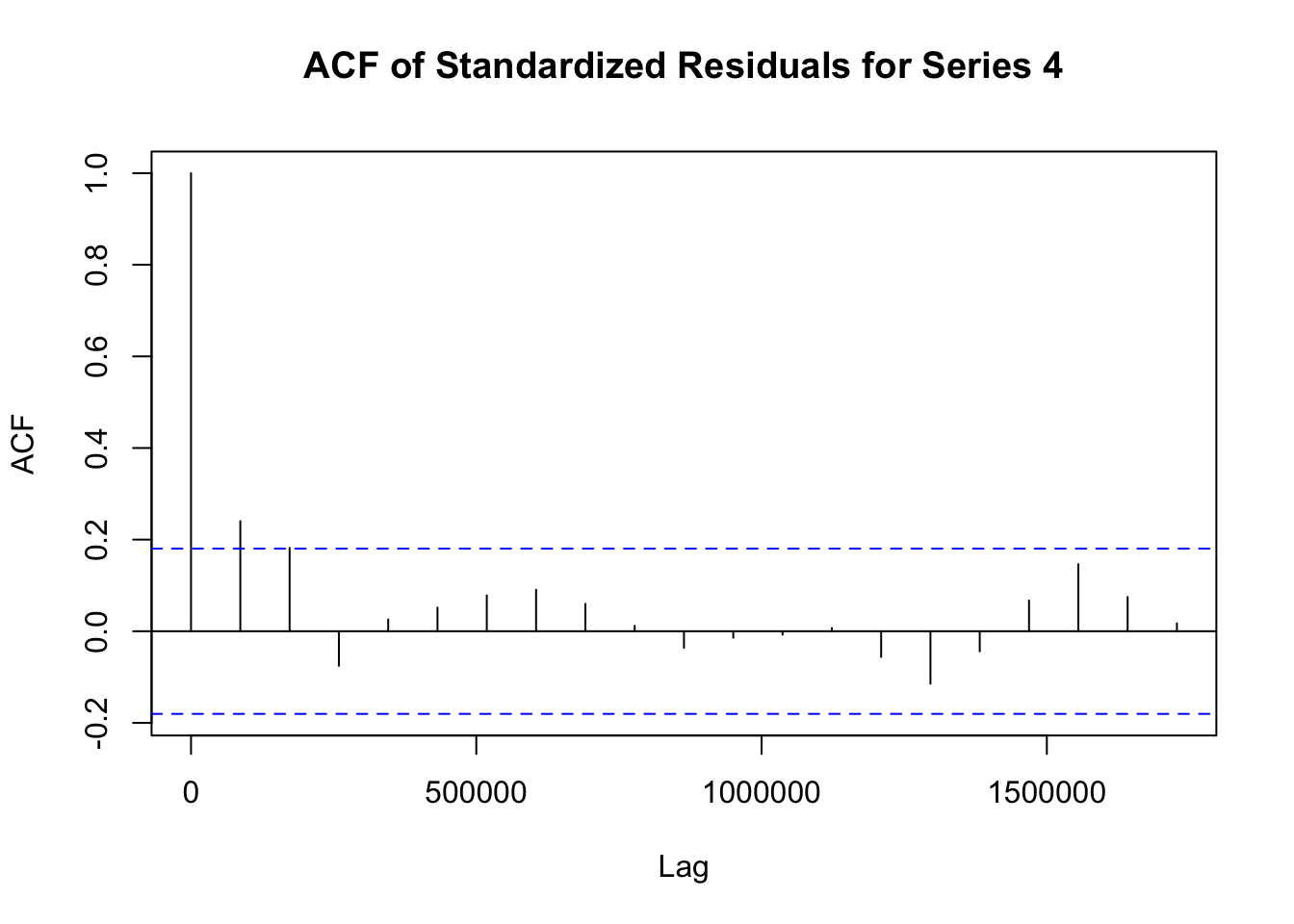
# 提取 fit_adcc 模型的标准化残差
std_residuals_fit_adcc <- residuals(fit_adcc)
# 对 fit_adcc 模型每个序列的标准化残差绘制自相关函数图
for (i in 1:ncol(std_residuals_fit_adcc)) {
acf(std_residuals_fit_adcc[, i], main = paste("ACF of Standardized Residuals for Series", i))
}